Электр тербелістері индуктивтілігі мен сыйымдылығы бар тізбекте пайда бола алады. Мұндай тізбек тербелмелі контур деп аталады. Тербелмелі контурдағы зарядтың өзгеруі мына өрнек арқылы сипатталады:

мұнда

контурдың меншікті жиілігі деп аталады.
Конденсатордағы зарядтың өзгеру заңдылығы мынадай болып шығады:
q = qm cos(ω0t+φ0)
Кез келген нақты контурдың актив кедергісі болады. Контурдағы энергия осы кедергі арқылы біртіндеп шығындалады. Осының салдарынан еркін тербелістер өшетін болады. Конденсатодағы зарядтың өзгерісі үшін мына теңдеді аламыз:

мұның шешуі мынаған тең болады:
q = qme-βt cos(ωt +φ0)
мұнда β = R / (2L) өшу коеффициенті деп аталады. Өшетін тербеліс жиілігі өшпейтін ерікті тербеліс жиілігінен кем болады:
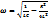
Өшетін тербелістерді сипаттау үшін, контурдың сапалығы (мықтылығы) деген шама енгізіледі:
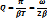
Өшпейтін ербелістер алу үшін жүйеге периодты өзгеріп тұратын сырттай әсер беру керек. Бұл кезде еріксіз тербелістердің дифференциалдды теңдеуі былай жазылады:
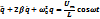
Бұл теңдеудің дербес шешулері мына түрде болады:
q = qm cos (ωt – ψ)
мұндағы

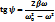
Мәжбүрлеуші әсердің жиілігі жүйенің меншікті жиілігіне жақындағанда тізбекте резонанс құбылысы байқалады. Бұл кезде тізбектегі ток пен конденсатордағы кернеу күрт артады. Резонансты қисықтың салыстырмалы ені Контур сапалылығына кері шама болады:

Өшпейтін тербелістер алу үшін лампылы немесе транзисторлы автотербелмелі жүйелер қолднылады.
Электромагниттік толқындар. Толқын жылдамдығы. Өріс энергиясы. Пойнтинг векторы. Электромагниттік толқындарды байланыс құралы мақсатында қолдану.
Максвелл теңдеулерінің токтар мен зарядтар жоқ жердегі дифференциалды түрі мындай болады:

divD=0

divB=0
Бұл теңдеулерге rot операияын қолданып мына теңдеуді аламыз:

Дәл осындай теңдеуді өріс кернеулігі үшін де жаза аламыз. Бұл теңдеу жылдамдығы

болатын толқынды сипаттайды, яғни электр (магнит) өрісі кеңістікте толқын түрінде таралады. Вакуумде электромагниттік толқындар 3·108м/с жылдамдықпен таралады. Кеңістіктің аз аймақтары үшін электромагниттік толқындарды жазық деп қарастыруға болады. Х өсінің бойымен тараалатын тоқын үшін мына теңдеулерді аламыз:
E = Em cos(ωt + kx)
H = Hm cos(ωt + kx)
мұнда ω–толқын жиілігі, k–тоқындық сан. Е және Н векторлары толқынның таралу бағытымен оң бұрандалық жүйе құрайды. Электромагиттік өріс энергиясы электр және магнит өрістері энергияларының қосындысынан тұрады:

Электромагнит өріс энергиясын энергия ағынының тығыздығы арқылы сипаттауға болады. Ол Пойнтинг векторы арқылы өрнектеледі:
S = [ E H ]






