Рассмотрим как критерий Колмогорова (λ) применяется при проверке гипотезы о нормальном распределении генеральной совокупности. Выравнивание фактического распределения по кривой нормального распределения состоит из нескольких этапов:
- Сравнивают фактические и теоретические частоты.
- По фактическим данным определяют теоретические частоты кривой нормального распределения, которая является функцией нормированного отклонения.
- Проверяют на сколько распределение признака соответствует нормальному.



Для IV колонки таблицы:
В MS Excel нормированное отклонение (t) рассчитывается с помощью функции НОРМАЛИЗАЦИЯ. Необходимо выделить диапазон свободных ячеек по количеству вариант (строк электронной таблицы). Не снимая выделения, вызвать функцию НОРМАЛИЗАЦИЯ. В появившемся диалоговом окне указать следующие ячейки, в которых размещены, соответственно, наблюдаемые значения (Xi), средняя (X) и среднеквадратическое отклонение Ϭ. Операцию обязательно завершить одновременным нажатием клавиш Ctrl+Shift+Enter
ДляV колонки таблицы:
Функцию плотности вероятности нормального распределения φ(t) находим по таблице значений локальной функции Лапласа для соответствующего значения нормированного отклонения (t)
Для VI колонки таблицы:
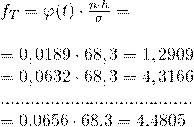
Критерий согласия Колмогорова (λ) определяется путем деления модуля max разности между эмпирическими и теоретическими кумулятивными частотами на корень квадратный из числа наблюдений:

По специальной таблице вероятности для критерия согласия λ определяем, что значению λ=0,59 соответствует вероятность 0,88 (λ<P) критерий статистически не значим. Это значит, что с вероятностью 0,88 можно судить, что отклонения фактических (эмпирических) частот от теоретических являются случайными. Следовательно, нулевая гипотеза принимается и есть основания утверждать, что эмпирическое распределение подчиняется нормальному распределению.
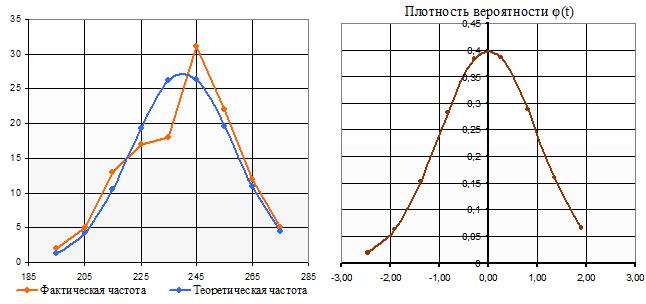
Распределение эмпирических и теоретических частот, плотности вероятности теоретического распределения
Применяя критерии согласия для проверки соответствия наблюдаемого (эмпирического) распределения теоретическому, следует различать проверку простых и сложных гипотез.
Одновыборочный критерий нормальности Колмогорова-Смирнова основан на максимуме разности между кумулятивным эмпирическим распределением выборки и предполагаемым (теоретическим) кумулятивным распределением. Если D статистика Колмогорова-Смирнова значима, то гипотеза о том, что соответствующее распределение нормально, должна быть отвергнута.




