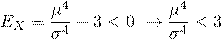Любое реальное распределение можно изобразить схематически в виде кривой, воспроизводящей основные особенности данного распределения. Под кривой распределения понимается графическое изображение в виде непрерывной линии изменения частот, функционально связанных с изменением вариант.
Элементами распределения являются:
- варианта
- частота
В зависимости от вида кривых, изображающих распределение, выделяют несколько основных типов распределения:
- одновершинные
- многовершинные
К одновершинным относятся те, в которых один, обычно центральный вариант, имеет наибольшую частоту (плотность распределения). Частоты же остальных вариантов убывают по мере удаления от центрального.
Если частоты убывают слева и справа от центрального значения одинаково, то такие распределения называются симметричными.
Если частоты убывают слева и справа от центра распределения с разной скоростью, то такие распределения называют асимметричными.
Многовершинные распределения — это распределения, в которых несколько центров, т. е. такие, у которых несколько максимумов частот.
Для однородных совокупностей, как правило, характерны одновершинные распределения.
Многовершинность распределения свидетельствует о неоднородности изучаемого явления. В этом случае необходимо произвести перегруппировку данных с целью выделения более однородных групп.
Выяснение общего характера распределения предполагает, наряду с оценкой его однородности, вычисление показателей асимметрии и эксцесса.
Кривые распределения бывают:
- симметричными
- асимметричными.
В зависимости от того, какая ветвь кривой распределения вытянута, различают:
- правостороннюю асимметрию
- левостороннюю асимметрию.
Для характеристики степени асимметрии двух или нескольких рядов пользуются коэффициентом асимметрии.
Для одновершинных распределений:

Более точным является коэффициент асимметрии, рассчитанный как отношение центрального момента третьего порядка (μ3) к среднеквадратическому отклонению в 3-й степени (Ϭ3):

1. Для симметричного распределения:

Соответственно, в симметричном распределении центральный момент 3-го порядка равен нулю (μ3=0), т. е. алгебраическая сумма отклонений отдельных значений признака (вариант), расположенных слева и справа от средней, равна нулю. График симметричного распределения симметричен относительно точки максимума.

Для несимметричных распределений центральные моменты нечетного порядка отличны от нуля:
2. Асимметрия положительна (As>0), если длинная часть кривой распределения расположена справа от моды (Мо). В этом случае соотношение между средней, медианой и модой нарушено:
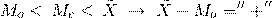

3. Асимметрия отрицательна (As<0), если длинная часть кривой распределения расположена слева от моды (Мо).


As< 0.25 – слабая асимметрия
As= 0.25-0.5 – умеренная асимметрия
As> 0.5 – крайне асимметричное распределение
Для оценки «крутизны» (островершинности) распределения пользуются характеристикой – эксцессом.
Коэффициент эксцесса:

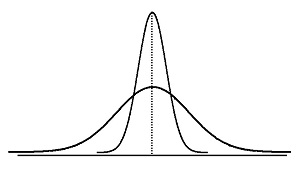
1. Для нормального распределения:

2. Выше нормального (островершинное распределение):

3. Ниже нормального (плосковершинное распределение):