Пространства функций можно считать обобщением пространства N-мерных сигналов – векторов на аналоговые сигналы, как бесконечномерные векторы, с некоторыми чисто практическими уточнениями.
Нормирование метрических параметров. Норма функций в пространстве L2[a, b] определяется выражением:
||s(t)|| = 
.
Нетрудно заключить, что чем больше интервал [a, b] в этой формуле, тем больше (при прочих равных условиях) будет значение нормы. При анализе и сравнении сигналов (как аналоговых, так и многомерных дискретных) такое понятие не всегда удобно, и вместо него очень часто используют понятие нормы, нормированной относительно длины интервала[a, b]. Для символьного обозначения нормирования будем применять знак Ñ:
||s(t)||Ñ = 
, ||sn||Ñ = 
.
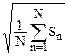Метрика сигналов (расстояние между сигналами) при аналогичном нормировании:
dÑ(s(t), v(t)) = 
, dÑ(sn, vn) = 
Эти выражения применяются для вычисления среднеквадратического расхождения сигналов или среднеквадратической погрешности выполнения какой-либо операции при сравнении ее результата с теоретически ожидаемым или априорно известным.
Нормированное скалярное произведение сигналов:
ás(t), v(t)ñÑ = 
s(t)v(t) dt = ||s(t)||Ñ ||v(t)||Ñ cos j.
ásn, vnñÑ =(1/N) 
sn vn = ||sn||Ñ ||sn||Ñ cos j.
Косинус угла (коэффициент корреляции) между сигналами – функциями не изменяет своих значений при вычислении как по нормированным, так и по ненормированным значениям скалярного произведения и нормы сигналов (значения нормировки в числителе и знаменателе выражения (2.1.8) сокращаются). Взаимная перпендикулярность функций определяется аналогично взаимной перпендикулярности векторов условием нулевого значения скалярного произведения.
Норма, метрика и скалярное произведение периодических функций обычно нормируются на длину главного периода Т.
Ортогональные сигналы. Два сигнала называются ортогональными (orthogonal), если имеют нулевое скалярное произведение:
áu(t), v(t)ñ = 
u(t)v(t) dt = 0.
Соответственно, два таких сигнала в своем функциональном пространстве являются взаимно перпендикулярными (угол между сигналами равен j = 90о), полностью независимыми друг от друга (некоррелированными, r = cos j = 0), и имеют нулевую энергию взаимодействия (Euv = 0).
На рисунке 2.3.1 приведены примеры взаимно ортогональных сигналов. Нулевое скалярное произведение двух левых сигналов обеспечивается их формой (равна нулю сумма положительных и отрицательных значений произведения сигналов), а двух правых - взаимным расположением (ненулевые значения сигналов не имеют общих координат).
Рис. 2.3.1. Ортогональные сигналы.
Попутно заметим, что энергия и мощность суммы ортогональных сигналов обладают свойством аддитивности, т.к. имеют нулевое значение скалярного произведения и, соответственно, энергии взаимодействия.
Ортонормированный базис пространства. Множество сигналов – векторов {vk, k = 1, 2, …, N} в N-мерном декартовом пространстве при единичной норме и выполнении условий взаимной ортогональности:
ávm, vnñ = 
(2.3.1)
могут быть приняты в качестве ортонормированного базиса данного пространства. Выражение (2.3.1) обычно записывается в следующей форме:
ávm, vnñ = dmn, (2.3.1')
где dmn – импульс Кронекера, равный правой части выражения (2.3.1).
С использованием ортонормированного базиса любой произвольный сигнал можно представить в виде линейной комбинации взвешенных базисных векторов:
s = c1v1 + c2v2 + … + cNvN,
где весовое значение сk определяется проекцией вектора s на соответствующее координатное направление:
ck = ás, vkñ.
При распространении данных положений на функциональное пространство L2[a, b] в качестве координатного базиса пространства мы должны использовать совокупность функций {u0(t), u1(t), u2(t), …}, в пределе - бесконечную, которая должна быть системой ортогональных функций {uk(t), k=0, 1, 2, …}, т.е. все функции на этом отрезке должны быть взаимно ортогональны:
áum(t), un(t)ñ = um(t) un(t) dt = 0, m = 1, 2,...; n = 1, 2,...; m ¹ n.
Система ортогональных функций на интервале [a, b] будет ортонормированной (orthonormal functions), если все функции системы при m=n имеют единичную норму, т.е. выполняются условия:
áum(t), um(t)ñ = ||um(t)||2 = (um(t))2 dt = 1, ||um(t)|| = 1, m = 1, 2,....
Эти условия можно записать в следующей обобщенной форме:
um(t)·un*(t) dt = dm,n.
Система ортогональных функций всегда может быть превращена в ортонормированную путем нормировки, т.е. деления всех функций на их норму.
Разложение сигнала в ряд. Произвольный сигнал s(t) Î H (пространство Гильберта), заданный на интервале [a, b], может быть разложен в ряд по упорядоченной системе ортонормированных базисных функций uk(t):
s(t) =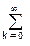 
ckuk(t). (2.3.2)
Для нахождения значений коэффициентов сk умножим обе части данного выражения на базисную функцию um(t) с произвольным номером m и проинтегрируем результаты по переменной t, при этом получим:
s(t)um(t) dt = 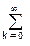ck umuk dt.
С учетом ортонормированности функций ui(t), в правой части этого равенства остается только один член суммы с номером m = k при ukuk dt =1, который, по левой части уравнения, представляет собой скалярное произведение сигнала и соответствующего m = k базисного вектора, т.е. проекцию сигнала на соответствующее базисное направление:
ck = s(t)uk(t) dt. (2.3.2)
Таким образом, в геометрической интерпретации коэффициенты сk представляют собой проекции вектор - сигнала s(t) на соответствующие базисные направления uk(t), т.е. координаты вектора s(t) по координатному базису, образованному системой ортогональных функций u(t), в пределе - бесконечномерной. При практическом использовании количество членов ряда (2.3.2) ограничивается определенным значением N, при этом для любого значения N совокупность коэффициентов ck обеспечивают наименьшее по средней квадратической погрешности приближение к заданному сигналу.
Соответственно, энергия взаимодействия двух сигналов x(t) и y(t) может вычисляться по скалярному произведению их координатных проекций, которое, с учетом взаимной ортогональности всех проекций, будет равно:
áx(t), y(t)ñ = x(t)y(t) dt = [ 
anun(t)] [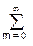 
bmum(t)] dt = an×bn. (2.3.3)
Косинус угла между векторами x(t) и y(t) с использованием выражения (2.3.3):
cos j = an×bn /(||x(t)||×||y(t)||).
Возможность разложения непрерывных сигналов и функций в обобщенные ряды по системам ортогональных функций имеет огромное принципиальное значение, так как позволяет вместо изучения несчетного множества точек сигнала ограничиться счетной системой коэффициентов ряда.
К системам базисных функций, которые используются при разложении сигналов, предъявляют следующие основные требования:
- для любого сигнала ряды разложения должны сходиться;
- при ограничении ряда по уровню остаточной погрешности расхождения с заданным сигналом количество членов ряда должно быть минимальным;
- функции должны иметь достаточно простую аналитическую форму;
- коэффициенты разложения должны вычисляться относительно просто.
Согласно теореме Дирехле, любой сигнал s(t), имеющий конечное число точек нарушения непрерывности первого рода и конечный по энергии на интервале [a, b], может быть разложен по системе ортонормальных функций, если существуют интегралы модуля сигнала и модуля его первой производной, т.е.:
|s(t)| dt < ¥, |s'(t)| dt < ¥.
Ортонормированные системы функций хорошо известны в математике. Это полиномы Эрмита, Лежандра, Чебышева, функции Бесселя, Лагерра и целый ряд других. Выбор типа функций в качестве координатного базиса сигнального пространства, как и координатных осей для обычного трехмерного пространства (декартовы, цилиндрические, сферические и пр.), определяется удобством и простотой последующего использования при математической обработке сигналов. При спектральном анализе сигналов используются, в основном, два вида ортонормированных функций: гармонические функции и функции Уолша.
На интервале [-p, p] рассмотрим систему следующих гармонических функций:
{1, sin t, sin 2t, …, sin kt}, k = 1, 2, 3, … (2.3.4)
Вычислим нормированные на интервал скалярные произведения системы:
á1, sin ktñ =(1/2p) 
sin kt dt = (1/2kp) [cos kp - cos(-kp)] = 0, k = 1, 2, 3, …
ásin mt, sin ntñ =(1/2p) sin mt sin nt dt =(1/4p) {cos (m+n)t – cos (m-n)t} dt =
= 
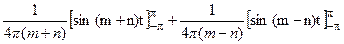= 0, при m ¹ n.
Следовательно, система (2.3.4) является системой взаимно ортогональных функций. Норма функций:
||sin kt||2=(1/2p) sin2 kt dt= (1/4p) (1-cos 2kt) dt=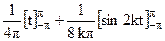 
=1/2.
||sin kt|| = 1/ 
, k = 1, 2, 3, …
Соответственно, для превращения системы (2.3.4) в ортонормированную следует разделить все функции системы на значение нормы (рис. 2.3.2):
{1, uk(t) = sin kt}, k = 1, 2, 3, … (2.3.4')
Рис. 2.3.2. Ортонормированный базис гармонических функций.
Аналогичным образом можно убедиться в ортонормированности косинусной системы гармонических функций:
{1, uk(t) = cos kt}, k = 1, 2, 3, …, (2.3.5)
и объединенной синус-косинусной системы:
{1, uk(t) = sin kt, uk(t) = cos kt}, k = 1, 2, 3, … (2.3.6)
Наибольшее распространение в качестве базисных функций частотного разложения нашли комплексные экспоненциальные функции exp(pt) при p = jf (преобразование Фурье) и p = s+jf (преобразование Лапласа), от которых с использованием формул Эйлера
exp(jwt) = cos(wt) + j sin(wt), exp(-jwt) = cos(wt) - j sin(wt),
cos(wt) = [ехр(jwt)+exp(-jwt)]/2, sin(wt) = [ехр(jwt)-exp(-jwt)]/2j
всегда можно перейти к синус-косинусным функциям. Термин "частотного" обязан своим происхождением независимой переменной частотного представления сигналов, которая измеряется в единицах, обратных единицам времени, т.е. в единицах частоты f = 1/|t|. Однако понятие частотного преобразования не следует связывать только с временным представлением сигналов, т.к. математический аппарат преобразования не зависит от физического смысла переменных. Так, например, при переменной "х", как единице длины, значение f будет представлять собой пространственную частоту - число периодических изменений сигнала на единице длины с размерностью 1/|х|.
Ортонормированная система функций Уолша, по существу, является предельной модификацией системы периодических функций с кратными частотами, при этом функции принимают значения только ±1. Пример четырех первых функций Уолша на интервале Т от –0,5 до 0,5 приведен на рис. 2.3.3. Ортогональность и нормированность функций следует из принципа их построения. Стандартное математическое обозначение функций Уолша: wal(k,х), где k = 0,1,2, … – порядковый номер функции, х = t/T – безразмерная координата (нормированная на интервал Т независимая переменная).
Наряду с функциями Уолша применяются также две связанные с ними системы: четные и нечетные функции cal(n,х) = wal(2n,х), – аналогичные косинусам, и sal(n,х) = wal (2n-1,х), – аналогичные синусам.
Рис. 2.3.3. Функции Уолша.
При разложении сигналов форма спектров Уолша практически тождественна спектрам гармонических функций.
Разложение энергии сигнала. Допустим, что сигнал s(t) разложен в обобщенный ряд Фурье (2.3.2). Вычислим энергию сигнала непосредственной подстановкой выражения (2.3.2) в выражение (2.2.2):
Es = 
s2(t) dt = 
cmcnumun dt = cmcn umun dt. (2.3.7)
В этом выражении в силу ортонормированности базисной системы отличны от нуля только члены с номерами m = n. Отсюда:
Es = s2(t) dt = cn2, (2.3.8)
т.е. при корректном разложении сигнала в обобщенный ряд Фурье энергия сигнала не изменяется, и равна сумме энергии всех составляющих ряда. Это соотношение называют равенством Парсеваля.
