Пространство сигналов [1,3,16,29]

СИГНАЛЫ и ЛИНЕЙНЫЕ СИСТЕМЫ

Тема 2: МЕТРОЛОГИЯ СИГНАЛОВ

Физическая величина более точно определяется уравнением, чем измерением.

Макс Планк. Немецкий физик – теоретик, XVIII-XIX в.

Между тем, уравнение только математическая модель физической величины. А без измерений понятия точности вообще не существует.

Борис Старцев. Уральский геофизик – практик, XX-XXI в.

Содержание: 2.1. Пространство сигналов. Линейное пространство сигналов. Норма сигналов. Метрика сигналов. Скалярное произведение сигналов. Коэффициент корреляции сигналов. Координатный базис пространства. 2.2. Мощность и энергия сигналов. Понятия мощности и энергии сигналов. 2.3. Пространства функций. Нормирование метрических параметров. Ортогональные сигналы. Ортонормированный базис пространства. Разложение сигнала в ряд. Ортонормированные системы функций. Разложение энергии сигнала. 2.4. Функции корреляции сигналов. Корреляционные функции сигналов. Взаимная корреляционная функция. 2.5. Математическое описание шумов и помех. Шумы и помехи. Природа помех. Характеристики помех. Литература.

ВВЕДЕНИЕ

В данной теме метрология сигналов рассматривается, в основном, на уровне понятий и базовых определений, предваряя их более подробное изучение в дальнейших темах курса. Это объясняется тем, что при детальном изучении каких-либо характеристик или свойств сигналов их рассмотрение не может выполняться в отрыве от других метрологических характеристик рассматриваемых типов сигналов и требует определенной ориентировки в общей метрологии сигналов, хотя бы на уровне понятий.

Пространство сигналов [1,3,16,29].

Важнейшее свойство аналоговых и дискретных сигналов заключается в том, что их линейные комбинации также являются аналоговыми или дискретными сигналами. Линейные комбинации цифровых сигналов, в силу их ограничения по разрядности, в принципе относятся к разряду нелинейных операций, однако последним фактором можно пренебречь, если ошибки, которые вносятся в результаты наблюдений при квантовании отсчетов, достаточно малы по сравнению с шумами зарегистрированной информации. При дискретизации и квантовании данных непосредственно на входах в ЭВМ последнее выполняется практически всегда, поскольку ошибки определяются разрядностью ЭВМ и программными системами обработки данных, которые обычно не ниже 6-12 десятичных разрядов.

Пространство сигналов. Пусть L{s₁(t), s₂(t), …} - множество сигналов, которые имеют какие-то общие свойства и определенную структуру связи между сигналами. Например, множество может состоять из сигналов вида s_n(t) = A_ncos(w_nt+j_n)·exp(-at²) – затухающих гармонических колебаний с определенными значениями амплитуд, частот и начальных фаз. Путем введения структурных ограничений множество сигналов может быть превращено в функциональное пространство сигналов. Так, если пространство значений независимой переменной t задано выражением R:=(-¥,+¥), то пространство сигналов L^p[R] определяет множество сигналов в этом пространстве, для которых выполняется условие однозначной реализации:

|s(t)|^p dt < ¥.

Для анализа сигналов наиболее часто используется гильбертово пространство, сигналы в котором должны удовлетворять условию интегрирования с квадратом:

|s(t)|² dt < ¥.

Периодические сигналы обычно рассматриваются в пространстве L²[0,2p] одного периода:

|s(t)|² dt < ¥.

Линейное пространство сигналов. Множество сигналов L образует линейное пространство сигналов, если для него справедливы следующие аксиомы:

1. Для любых сигналов u(t) Î L и v(t) Î L существует их сумма s(t) = u(t)+v(t), которая также содержится в L. Операция суммирования коммутативна: u(t)+v(t) = v(t)+u(t), и ассоциативна: u(t)+(v(t)+x(t)) = (u(t)+v(t))+x(t).

2. Для любого сигнала s(t) Î L и числа a определен сигнал y(t) = as(t), у(t) Î L.

3. Множество L содержит такой нулевой элемент Æ, что для всех сигналов u(t) Î L выполняется равенство u(t)+Æ = u(t).

Пример. Множество сигналов L состоит из импульсных сигналов произвольной формы с амплитудой не более 10 вольт. Образуют ли эти сигналы линейное пространство?

Нет, не образуют, так как не выполняется, по крайней мере, первая аксиома линейного пространства (сумма двух сигналов с амплитудой более 5 вольт превышает 10 вольт). Требуются дополнительные структурные ограничения по параметрам сигналов.

Сигналы могут описываться как вещественными, так и комплексными функциями, и линейные пространства также могут быть вещественными или комплексными.

Множество L, для которого выполняются данные аксиомы, при анализе сигналов и систем может рассматриваться как специальным образом сконструированное многомерное (в пределе – бесконечномерное) геометрическое пространство. Сигналы таких линейных пространств называют векторами в силу аналогии их свойств со свойствами векторов. Рассмотрим это на конкретном примере.

Представим себе произвольный сигнал s(t), заданный на интервале [a, b]. Дискретизируем сигнал с равномерным шагом дискретизации и переведем в цифровую форму (представим N последовательными выборками):

s = (s₁, s₂, …, s_N).

В таком представлении величина s может рассматриваться в виде N-мерного вектора в N-мерном пространстве, в котором значения s_n представляют собой проекции s-вектора на координатные оси данного пространства. Двумерный вектор в двумерном пространстве – это точка с координатами s₁ и s₂ на рис. 2.1.1. Соответственно, в трехмерном пространстве сигнал s представлен точкой в трехмерном пространстве. Представить себе N-мерное пространство при N>3 можно только абстрактно, но с математических позиций такое пространство вполне реально и N-мерный сигнал s отображается вполне определенной точкой в этом пространстве с координатами s_n по осям пространства. При уменьшении интервала дискретизации сигнала до бесконечно малой величины значение N стремится к бесконечности, и пространство сигналов превращается в бесконечномерное пространство аналоговых сигналов. Следовательно, и аналоговые сигналы могут рассматриваться как предельный случай бесконечномерных векторов.

Рис. 2.1.1. Пространства сигналов и функций.

С учетом вышеизложенного, для математического анализа систем и сигналов в линейном пространстве может использоваться математика векторов. Основными метрическими параметрами векторного анализа являются норма, метрика и скалярное произведение сигналов.

Норма сигналов в линейном пространстве является аналогом длины векторов и обозначается индексом ||s(t)|| - норма (norm). В математике существуют различные формы норм. При анализе сигналов обычно используются квадратичные нормы:

||s(t)|| = . (2.1.2)

Соответственно, для дискретных сигналов:

||s(t)|| = . (2.1.2')

Для комплексных сигналов:

||s(t)|| = , (2.1.2'')

где s*(t) – величины, комплексно сопряженные с s(t).

Линейное пространство сигналов L является нормированным, если каждому сигналу пространства s(t) однозначно сопоставлена его числовая норма ||s(t)||, и выполняются следующие аксиомы:

1. Норма неотрицательна и равна нулю тогда и только тогда, когда сигнал равен нулю (||s(t)|| = Æ, при s(t) = Æ).

2. Для любого числа b должно быть справедливо равенство: ||bs(t)|| = |b| × ||s(t)||.

3. Если v(t) и u(t) – сигналы из пространства L, то должно выполняться неравенство треугольника: ||v(t)+u(t)|| £ ||v(t)|| + ||u(t)||.

Пример норм для двумерных цифровых сигналов приведен на рис. 2.1.2.

Рис. 2.1.2. Норма и метрика сигналов.

Метрика сигналов. Линейное пространство сигналов L является метрическим, если каждой паре сигналов s(t) Î L и v(t) Î L однозначно сопоставляется неотрицательное число r(s(t),v(t)) – метрика (metric) или расстояние между векторами. Пример метрики для двух векторов в двумерном пространстве приведен на рис. 2.1.2.

Для метрик сигналов в метрическом пространстве любой размерности должны выполняться аксиомы:

1. r(s(t),v(t)) = r(v(t),s(t)) – рефлексивность метрики.

2. r(s(t),s(t)) = 0 для любых s(t) Î L.

3. r(s(t),v(t)) £ r(s(t),a) + r(a,v(t)) для любых a Î L.

Метрика определяется нормой разности двух сигналов (см. рис. 2.1.2):

r(s(t),v(t)) = || s(t) – v(t) ||. (2.1.3)

В свою очередь норму можно отождествлять с расстоянием от выбранного элемента пространства до нулевого: ||s(t)|| = r(s(t),Æ).

По метрике сигналов можно судить, например, о том, насколько точно один сигнал может быть аппроксимирован другим сигналом, или насколько изменяется выходной сигнал относительно входного при прохождении через какое-либо устройство.

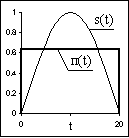Рис. 2.1.3.

Пример. Сигнал на интервале (0,Т) представляет собой половину периода синусоиды амплитудой A: s(t) = A×sin(pt/T), 0 £ t £ T. Требуется аппроксимировать сигнал прямоугольным импульсом п(t) (см. рис. 2.1.3).

Если принять амплитуду импульса п(t) равной В, то квадрат расстояния между сигналами: r²(s,п) = (A sin(pt/T)-В)² dt = A²T/2 - 4ABT/p + B²T.

Для решения задачи требуется найти минимум выражения r²(s,п). Дифференцируем полученное выражение по В, приравниваем нулю и, решая относительно В, находим значение экстремума: В = 2A/p» 0.64А. Это искомое значение минимума функции r²(s,п), так как вторая производная функции по В положительна. При этом минимальное значение метрики: r_min» 0.31A . Вычислим нормы сигналов при А = 1:

Е_s = А² sin² (pt/T) dt = A² T/2 = 10. Норма: ||s(t)|| = = 0.707 A » 3.16.

Е_п = B² dt = B² T» 8.1. Норма: ||п(t)|| = = B » 2.85.

Скалярное произведение произвольных сигналов u(t) и v(t) отражает степень их связи (сходства) по форме и положению в пространстве сигналов, и обозначается как áu(t), v(t)ñ.

áu(t), v(t)ñ = ||u(t)||×||v(t)|| cos j, (2.1.4)

Физическую сущность скалярного произведения векторов в двумерном пространстве можно видеть достаточно наглядно (рис. 2.1.4). Это произведение "длины" (нормы) одного вектора на проекцию второго вектора по "направлению" первого вектора.

Рис. 2.1.4. Скалярное произведение сигналов в двумерном пространстве.

При кажущейся абстрактности скалярного произведения сигналов оно может приобретать вполне конкретный физический смысл для конкретных физических процессов, которые отображаются этими сигналами. Так, например, если v = F – сила, приложенная к телу, а u = s – перемещение тела под действием этой силы, то скалярное произведение W = F·s определяет выполненную работу, при условии совпадения силы с направлением перемещения. В противном случае, при наличии угла j между векторами силы и перемещения, работа будет определяться проекцией силы в направлении перемещения, т.е. W = s·F·cos j.

Вычисление скалярного произведения обычно производится непосредственно по сигнальным функциям. Поясним это на примере двумерных сигналов с использованием рисунка 2.1.2. Для квадрата метрики сигналов s и v имеем:

||s-v||² = ||s||² + ||v||² – 2 ||s|| ||v|| cos j = ||s||² + ||v||² – 2 ás, vñ.

2 ás,vñ = ||s||² + ||v||² - ||s-v||² = (s₁²+s₂²)+(v₁²+v₂²)–{(s₁-v₁)²+(s₂-v₂)²} = 2 (s₁v₁+s₂v₂).

ás,vñ = s₁v₁+s₂v₂.

Обобщая полученное выражение на аналоговые сигналы:

ás(t), v(t)ñ = s(t)v(t) dt. (2.1.5)

Соответственно, для дискретных сигналов в N-мерном пространстве:

ás_n, v_nñ = s_n v_n. (2.1.5')

Скалярное произведение обладает следующими свойствами:

1. ás,vñ ³ 0;

2. ás,vñ = áv,sñ;

3. áas,vñ = aás,vñ, где а – вещественное число;

4. ás+v, añ = ás,añ + áv,añ.

Линейное пространство аналоговых сигналов с таким скалярным произведением называется гильбертовым пространством Н (второе распространенное обозначение - L₂). Линейное пространство дискретных и цифровых сигналов - пространством Евклида (обозначение пространства - R₂). В этих пространствах справедливо фундаментальное неравенство Коши-Буняковского (модуль косинуса в (2.1.4) может быть только равным или меньше 1):

|ás,vñ| £ ||s||×||v||. (2.1.6)

Для комплексного гильбертова пространства скалярное произведение вычисляется по формуле:

ás(t), v(t)ñ = s(t)v*(t) dt. (2.1.7)

При определении функций в пространстве L²[a,b] вычисление скалярного произведения производится соответственно с пределами интегрирования от а до b.

Из выражения (2.1.4) следует косинус угла между сигналами:

cos j = ás(t),v(t)ñ /(||s||×||v||). (2.1.8)

Пример. Имеется два смещенных во времени прямоугольных импульса с одинаковой амплитудой и длительностью: s₁(t) = 2 при 0 £ t £ 5, s₁(t) = 0 при других t; и s₂(t) = 2 при 4 £ t £ 9, s₂(t) = 0 при других t.

Квадраты норм сигналов: ||s₁||² = s₁²(t)dt = 20. ||s₂||² = s₂²(t)dt = 20

Скалярное произведение: ás₁,s₂ñ = s₁(t) s₂(t) dt = 8.

Отсюда имеем: cos j = (s₁,s₂)/ (||s₁||×||s₂||) = 8/20 = 0.4 и j» 1.16 радиан» 66^о

При полном совмещении сигналов: ás₁,s₂ñ = s₁(t) s₂(t) dt = 20, cos j = 1, j = 0.

При отсутствии перекрытия сигналов; ás₁,s₂ñ = 0, cos j = 0, j = 90^о.

Физическое понятие "угла" между многомерными сигналами довольно абстрактно. Однако при рассмотрении выражения (2.1.8) совместно с выражением для квадрата метрики сигналов

r²(s,v) = [s(t)-v(t)]² dt = ||s||² + ||v||² - 2×||s||×||v|| cos j.

можно отметить следующие закономерности. При j = 0 (cos j = 1) сигналы "совпадают по направлению" и расстояние между ними минимально. При j = p/2 (cos j = 0) сигналы "перпендикулярны друг другу" (иначе говоря – ортогональны), и проекции сигналов друг на друга равны 0. При j = p (cos j = -1) сигналы "противоположны по направлению" и расстояние между сигналами максимально. Фактор расстояния между сигналами играет существенную роль при их селекции в многоканальных системах.

Коэффициент корреляции сигналов. Одновременно заметим, что значение косинуса в (2.1.8) изменяется от 1 до -1, и не зависит от нормы сигналов ("длины" векторов). Максимальное значение cos j = 1 соответствует полной тождественности относительной динамики сигналов, минимальное значение cos j = -1 наблюдается при полной противоположности значений относительной динамики сигналов. По существу, коэффициент r = cos j является интегральным коэффициентом степени сходства формы сигналов по пространству их задания. С учетом этого он и получил название коэффициента корреляции сигналов. На рис. 2.1.5 можно наглядно видеть значения коэффициента корреляции двух сигналов в зависимости от их формы и сдвига по независимой переменной.

Рис. 2.1.5. Коэффициент корреляции сигналов.

Однако количественные значения коэффициентов корреляции существенно зависят от выбора нулевой точки сигнального пространства. Рассмотрим это более детально на конкретном примере.

На рис. 2.1.6 приведено изменение средней месячной температуры воздуха в трех городах земного шара в течение одного календарного года. Характер корреляции между изменениями температур в городах достаточно хорошо виден на графиках. Вычислим (см. пример ниже) значения коэффициентов корреляции для шкалы температур по Цельсию.

Рис. 2.4.1.

Пример. Среднемесячная температура воздуха в городах по Цельсию:

Екатеринбург: E_k = {-12,-10,-4,5,11,19,23,21,15,5,-3,-8}. Дели: D_k = {15,18,22,28,33,35,33,32,30,28,21,17}.

Буэнос - Айрес: B_k = {26,24,21,18,14,11,10,10,12,15,20,23}. Нумерация месяцев: k = 1, 2, 3, …, 12.

Норма сигналов: ||E|| = = 45.39, ||D|| = = 93.05, ||B|| = = 61.9.

Скалярные произведения: áE, Dñ = = 2542, áE, Bñ = 268, áB, Dñ = 4876.

Коэффициенты корреляции: Екатеринбург – Дели: r _ED = áE, Dñ / (||E|| ||D||) = 0.602.

Екатеринбург – Буэнос-Айрес: r _EB = 0.095, Дели – Буэнос-Айрес: r _DB = 0.847,

Как следует из вычислений, полученные коэффициенты корреляции маловыразительны. Практически не регистрируется разнонаправленная корреляция Екатеринбург - Буэнос-Айрос, и не различаются одно- (Екатеринбург – Дели) и разнонаправленные (Дели – Буэнос-Айрос) типы корреляции.

Повторим вычисления в шкале Фаренгейта (0^оF = -17,8^oC, 100^oF = +37,8^oC), и в абсолютной шкале температур Кельвина. Дополнительно вычислим значения коэффициентов корреляции в шкале Цельсия и Фаренгейта для центрированных сигналов. Центрированный сигнал вычисляется путем определения среднего значения сигнала по интервалу его задания и вычитания этого среднего значения из исходных значений сигнала, т.е. среднее значение центрированного сигнала равно нулю. Сводные результаты вычислений приведены в таблице.

Таблица 2.1.1.

Коэффициенты корреляции сигналов

Пары городов	Нецентрированные сигналы	Центрированные сигналы
Цельсий	Фаренгейт	Кельвин	Цельсий	Фаренгейт
Екатеринбург – Дели Екатеринбург – Буэнос-Айрес Дели – Буэнос-Айрес	0.602 0.095 0.847	0.943 0.803 0.953	0.998 0.999	0.954 -0.988 -0.960	0.954 -0.988 -0.960

Как видно из таблицы, значения коэффициента корреляции нецентрированных сигналов существенно зависят от положения сигналов относительно нулевой точки пространства. При одностороннем смещении сигналов относительно нуля (шкала Фаренгейта) значение коэффициента корреляции может быть только положительным, и тем ближе к 1, чем дальше от сигналов нулевая точка (шкала Кельвина), т.к. при больших значениях сигналов-векторов значение скалярного произведения сигналов стремится к значению произведения норм сигналов.

Для получения значений коэффициентов корреляции, независимых от нуля сигнального пространства и от масштаба единиц измерений, необходимо вычислять коэффициент по центрированным сигналам, при этом в оценках коэффициента, как это видно из результатов, приведенных в таблице, появляется знаковый параметр совпадения (или несовпадения) по "направлению" корреляции и исчезает зависимость от масштаба представления сигналов. Это позволяет вычислять коэффициенты корреляции различных сигналов вне зависимости от физической природы сигналов и их величины.

Координатный базис пространства. Для измерения и отображения одномерных величин достаточно одного нормированного параметра – стандарта величины или единицы ее измерения (для измерения длины – сантиметр, для измерения тока – ампер, и т.п.).

В пространстве сигналов роль такого метрологического стандарта выполняет координатный базис пространства - подмножество векторов {е₁, е₂, е₃, …} со свойствами ортогональных координатных осей, по которым можно разложить любой произвольный сигнал, принадлежащий этому линейному пространству.

Совокупность векторов e_i пространства L является линейно независимой и образует координатный базис пространства, если равенство a_ie_i = Æ выполняется только в случае одновременного обращения в нуль всех числовых коэффициентов a_i. При этом произвольный сигнал s(t) может быть разложен по координатному базису e_i в виде

s(t) = с_ie_i, (2.1.9)

где числа с_i – проекции сигнала s(t) на координатный базис.

Число базисных векторов определяет размерность векторного пространства. Так, для двумерных векторов в качестве ортогонального базиса пространства могут быть приняты векторы {v₁, v₂}, если выполняется условие их взаимной перпендикулярности – нулевое значение скалярного произведения áv₁, v₂ñ = 0. При ||v₁|| = ||v₂|| = 1 эта пара векторов является ортонормированным базисом с единичными векторами координатных осей в качестве стандарта (единицы измерения) пространства.

Пример. Могут ли быть приняты в качестве координатного базиса двумерного пространства векторы

v₁ = ( /2, 1/2), v₂ = (-1/2, /2).

áv₁, v₂ñ = ( /2)·(-1/2) + (1/2)·( /2) = 0. Векторы ортогональны.

||v₁|| = = 1.

||v₂|| = = 1. Векторы нормированы.

Векторы могут быть ортонормированным базисом пространства.

Разложение произвольного двумерного вектора - сигнала s в двумерном пространстве по координатным осям элементарно:

s = c₁v₁ + c₂v₂, (2.1.10)

где коэффициенты с₁ и с₂ выражают значения составляющих вектора s по направлениям векторов v₁ и v₂, т.е. являются проекциями вектора s на координатный базис пространства {v₁, v₂}. Значения проекций определяются скалярными произведениями:

c₁ = ás, v₁ñ, c₂ = ás, v₂ñ.

В последнем нетрудно убедиться, если вычислить скалярные произведения левой и правой части выражения (2.1.10) сначала с вектором v₁:

ás, v₁ñ = á(c₁v₁+c₂v₂), v₁ñ = áс₁v₁, v₁ñ + áс₂v₂, v₁ñ = с₁áv₁, v₁ñ + с₂áv₂, v₁ñ.

При ортонормированности базиса {v₁, v₂} имеем:

áv₁, v₁ñ = ||v₁||² = 1, áv₂, v₁ñ = 0.

Отсюда следует: ás, v₁ñ = с₁. Аналогичным образом можно получить и выражение для значения c₂ = ás, v₂ñ.

Пример. Разложить вектор s = ( /2, 5/2) по базису, представленному векторами

v₁ = ( /2, 1/2) и v₂ = (-1/2, /2) из предыдущего примера.

s = c₁v₁ + c₂v₂.

с₁ = ás, v₁ñ = ( /2)·( /2) + (5/2)·(1/2) = 2.

с₂ = ás, v₂ñ = ( /2)·(-1/2) + (5/2)·( /2) = .

Результат: В пространстве с базисом {v₁, v₂} вектор s однозначно определяется двумя векторами v₁ и векторами v₂. s = 2v₁ + v₂.