Для получения дифференциальных уравнений движения воспользуемся уравнениями равновесия Эйлера в виде (2.1), а также принципом Даламбера, который заключается в следующем: если в систему уравнений равновесия прибавить силы инерции, взятые с обратным знаком, то эти уравнения будут описывать уже процесс движения жидкости.
Силы давления и массовые силы в уравнениях Эйлера отнесены к единице массы. Если выражение для силы инерции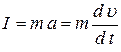 
отнести к единице массы, то получим в проекциях на оси координат
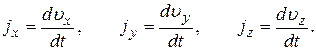
Тогда система дифференциальных уравнений движения невязкой жидкости, называемая также системой Эйлера, будет иметь вид
| (3.10) |
Напомним, что равномерное движение – это частный случай установившегося движения, характеризующийся тем, что по длине потока площадь трубы ω = const, а так как расход тоже постоянный, т. е. Q = const, то и скорость потока 
= const. Несмотря на такую, казалось бы, простоту, этот частный случай широко реализуется и для равномерных потоков в трубопроводах, и для неравномерного медленно меняющегося движения.
Рассмотрим равновесие отсека жидкости, движущейся в трубопроводе (рис. 3.18).
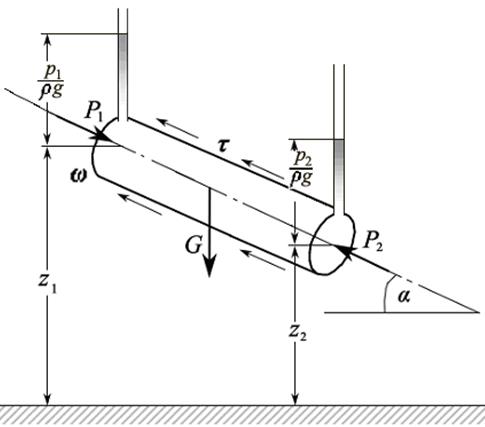
Рис. 3.18
Как известно, равномерное прямолинейное движение – это один из случаев равновесия. А согласно первому закону Ньютона, если тело находится в равновесии, то сумма всех сил, действующих на него, равна нулю.
Будем считать, что весь механизм трения сосредоточен на поверхности соприкосновения потока со стенками трубопровода, внутреннее трение в массиве жидкости учитывать не будем.
Тогда силы трения на стенках будут равны:
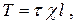
где τ – касательное напряжение трения;
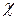– смоченный периметр;
l – длина рассматриваемого отсека.
Помимо сил трения на рассматриваемый отсек действуют силы давления P 1 и P 2 – по оси движения, а такжесила тяжести жидкости в отсеке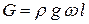 
.
Составим уравнение равновесия, т. е. равенства нулю сил, действую-щих на жидкость, в проекции на ось движения:
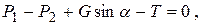
или
где
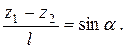
Разделим это уравнение на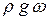 
. Получим:
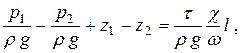
или
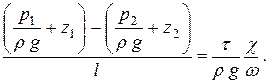
Левая часть равенства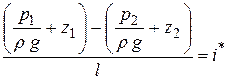 
– это пьезометри-ческий уклон. Отношение 
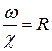– гидравлический радиус. Окончательно получаем
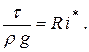
| (3.11) |
В случае равномерного движения пьезометрический уклон равен гидравлическому. Тогда получаем
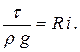
| (3.12) |
Это и есть основное уравнение равномерного движения жидкости.
