Водомер Вентури
В качестве примера использования уравнения Бернулли рассмотрим работу так называемого пьезометрического водомера (водомера Вентури). Он представляет собой сужение на трубопроводе, в которое включены пьезометры (рис. 3.11).
Рис. 3.11
Пусть известны диаметры труб d 1и d 2 в сечениях и отметки свободной поверхности в пьезометрах 
и 
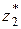. Требуется найти расход Q жидкости, протекающей по трубопроводу, пренебрегая потерями.
Уравнение Бернулли для первого и второго сечений потока
Очевидно, что
Обозначив разность – 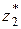= h, получим
Подставляя
будем иметь
Обозначив отношение площадей 
, определим расход
.
Если мы хотим выразить расход через параметры второго сечения, то, рассуждая аналогично, находим:
,
здесь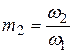 
.
Иногда для учета потерь в эти формулы вводят коэффициент 
(порядка 0,97 – 0,99).
Измеряют расход жидкости, протекающей по трубопроводу, также с помощью диафрагмы, устанавливаемой в сечении трубы. Принцип измерения тот же – при резком изменении диаметра проходного сечения меняется скорость течения. В соответствии с уравнением Бернулли изменяется давление, и разность пьезометрических напоров измеряется либо пьезометрами, либо дифференциальным манометром (рис. 3.12).
Рис. 3.12
Трубка Пито
Устройство, называемое «трубка Пито», используется для измерения скоростей потока жидкости.
В некоторой точке потока установим две трубки (рис. 3.13): обычную трубку пьезометра и открытую сверху трубку, нижний конец которой изогнут навстречу течению так, что его ось совпадает с направлением скорости. Диаметры трубок должны быть значительно меньше характерных размеров потока, чтобы не вносить больших искажений в распределение скоростей.
Составим уравнение Бернулли для двух сечений: проходящего через точку B – нижний конец пьезометра, и проходящего через точку A – носик изогнутой трубки.
.
Расположим нижний конец пьезометра и носик изогнутой трубки на одной горизонтали, тогда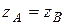 
. Носик изогнутой трубки является критической точкой, линия тока упирается в него и скорость потока в этой точке равна нулю (укрупненная врезка на рис. 3.13).
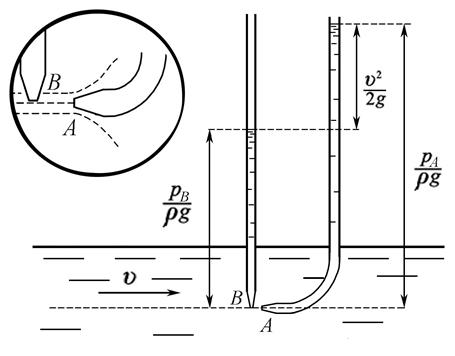
Рис. 3.13
Тогда уравнение Бернулли приобретет вид
.
Правая часть этого уравнения характеризует высоту подъема жидкости в изогнутой трубке. Из уравнения видно, что эта высота будет больше высоты столба жидкости в пьезометре на величину скоростного напора в точке B – у нижнего конца пьезометра. Сближая пьезометр и изогнутую трубку, можно определить значения скорости в непосредственной близости от носика трубки. Обозначив 
, получим 
, откуда
.
Действительная конструкция прибора для измерения скорости потока жидкости – трубки Пито – показана на рис. 3.14.
Рис. 3.14
Две трубки помещены в один корпус. Центральная динамическая трубка воспринимает полный напор 
, а наружная статическая трубка – только пьезометрический напор, так как скорость потока направлена по касательной к плоскости отверстий. Обе трубки подключены к дифференциальному манометру, который определяет разность напоров в трубках h, равную скоростному напору.
Струйные насосы (эжекторы)
Водоструйные насосы (эжекторы) получили из-за простоты конструкции и безопасности работы весьма разнообразное применение.
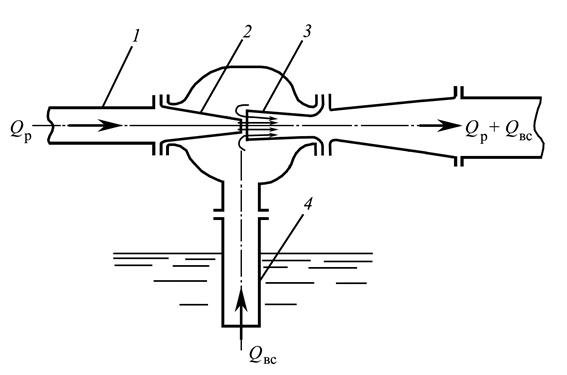
Рис. 3.15
Схема струйного насоса приведена на рис. 3.15. Для работы водоструйного насоса необходим еще один насос, который подает под большим давлением рабочий расход воды Q р. Из рабочего трубопровода 1 вода поступает в сопло 2, где из-за уменьшения площади сечения еще больше ускоряется. На выходе из сопла, благодаря значительному возрастанию скорости, давление в струе становится ниже атмосферного. За счет создающегося таким образом вакуума по всасывающей трубе 4 засасывается дополнительный расход жидкости Q вс. В камере 3 оба потока смешиваются и поступают в расширяющуюся трубу. Здесь скорость потока уменьшается, и кинетическая энергия в значительной части переходит в потенциальную энергию давления, под действием которого суммарный расход жидкости 
перемещается далее по напорному трубопроводу. Давление, развиваемое водоструйным насосом, меньше давления, создаваемого рабочим насосом, но расход больше. Всасываемый расход Q вс может быть равен рабочему расходу Q р и даже превосходить его в 1,5 – 2 раза.
На том же принципе основано действие пневматических перегрузочных устройств для сыпучих грузов. Примером эжектора может служить и бытовой пульверизатор, в котором поток воздуха подсасывает и распыляет жидкость.
Свободная поверхность при сужении русла
Рассмотрим, что происходит с уровнем воды в реке или канале, если русло сужается по естественным причинам или при создании искусственных сооружений (мостовые опоры, вход в шлюз и проч.).
Участок сужения изображен на рис. 3.16 (а – вид в плане, б – участок сужения в разрезе).
Рис. 3.16
Выберем два сечения, проходящих по поверхности жидкости: сечение 1 – 1 на достаточном удалении от места сужения, сечение 2 – 2 непосредственно в месте сужения. На поверхности воды в обоих сечениях давление равно атмосферному:
.
Тогда уравнение Бернулли для этих сечений запишется так:
,
где z 1 и z 2 – расстояния от поверхности жидкости до горизонтального дна (глубина).
Поскольку расход воды в реке (канале) постоянен, очевидно, что 
, а, следовательно 
, т. е. в узком месте происходит понижение уровня движущейся жидкости.
То же явление наблюдается в реках на стремнинах и в водоворотах. Этим же объясняется и просадка уровня при входе судов в камеры шлюзов.
