Выделим при установившемся течении в движущейся жидкости элементарную струйку и отметим в ней два сечения – 1 – 1 и 2 – 2 (рис. 3.10). Площади этих сечений – ω 1и ω 2, координаты их центров тяжести – z 1и z 2соответственно.
Рис. 3.10
В момент времени t жидкость находится между сечениями 1 – 1 и 2 – 2. Она занимает объем, состоящий из отсеков I и III (рис. 3.10). Через промежуток времени dt жидкость переместится в новое положение и будет занимать объем, состоящий из отсеков III и II.
В соответствии с теоремой механики, приращение кинетической энергии системы за какой-то промежуток времени равно работе внешних сил за этот промежуток времени. При переходе из начального положения (жидкость занимает объем отсеков I и III) в последующее (отсеки II и III) при установившемся движении кинетическая энергия общего отсека III останется неизменной, поэтому приращение кинетической энергии произойдет за счет изменения энергии отсеков I и II.
Массы жидкости в отсеках определятся как
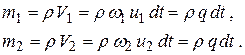
Здесь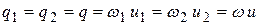 
– расход жидкости в струйке.
Оказывается, массы отсеков I и II равны, поэтому в дальнейшем индексы у обозначения массы опускаем. Тогда
| (3.4) |
Из внешних сил работу совершают поверхностные силы давления и массовые силы, в рассматриваемом случае это силы тяжести.
Из сил давления могут совершить работу только силы, действующие на торцевые сечения ω 1 и ω 2 – это силы P 1и P 2. Силы давления, действующие на боковые поверхности струйки, направлены перпендикулярно оси потока и их работа равна нулю. Работа сил давления
| (3.5) |
Работа сил тяжести состоит в том, что отсек I переместится в отсек II, поскольку отсек III остается на месте. Массы и, следовательно, веса отсеков одинаковы, поэтому работу сил тяжести можно записать как (вес равен 
):
 .
| (3.6) |
Приравнивая изменение кинетической энергии (3.4) сумме работ внешних сил (3.5) и (3.6), находим
Разделим все члены этого уравнения на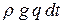 
. Таким образом, отнесем уравнение к единице веса протекающей жидкости. Получим
или
| (3.7) |
Это и есть уравнение Бернулли для элементарной струйки идеальной жидкости. Все члены уравнения имеют линейную размерность.
Из вывода понятен физический смысл уравнения Бернулли – оно является частным случаем закона сохранения энергии, а именно – отражает сохранение энергии частиц жидкости, движущихся вдоль линии тока.
Все члены уравнения (3.7) являются удельными энергиями, т. е. энергиями, отнесенными к единице веса протекающей жидкости. Член 
характеризует удельную кинетическую энергию потока, член 
– потенциальную энергию давления, а z – потенциальную энергию положения, которая равна высоте расположения частиц над условно выбранной плоскостью сравнения. Все вместе в сумме они дают полную (механическую) удельную энергию потока.
Таким образом, из уравнения Бернулли следует, что при движении частиц жидкости по длине элементарной струйки полная механическая энергия частиц (сумма удельных энергий) не изменяется.
Члены уравнения Бернулли имеют и другие названия, связанные с их линейной размерностью.
Член называется скоростным напором;
– пьезометрическим напором или пьезометрической высотой;
z – геометрическим напором или геометрической высотой.
Геометрический смысл уравнения Бернулли заключается в том, что сумма высот скоростного, пьезометрического и геометрического напоров есть величина постоянная.
Зачастую два члена уравнения Бернулли, характеризующие потенциальную энергию, объединяют в один, обозначив:
Тогда уравнение Бернулли запишется так:
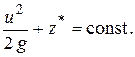
| (3.8) |
Напомним, что уравнение Бернулли выведено нами для идеальной жидкости (без учета вязкости). При рассмотрении реальной, т. е. вязкой жидкости, в балансе энергии необходимо учесть еще и потери энергии, обусловленные возникновением сил трения. Однако опыт показал, что, если силы трения малы по сравнению с массовыми силами, уравнение Бернулли для идеальной жидкости можно использовать для решения некоторых задач движения реальной жидкости.
