Аналитическое выражение для коэффициента динамичности не существует даже в простейшей постановке (без учета сил трения). Оценим его соотношение с одномассовой системой на примере.
Масса m2 ударяет со скоростью V по стержню, масса которого сосредоточена в точке 1. При этом 
. Сравниваем удар массой 
по невесомому стержню с ударом той же массой по стержню массой , сосредоточенной на одной трети его длины (см. рисунок).
В первом случае динамический прогиб точки удара
.
Вычислим значение максимального прогиба точки удара 
в двухмассовой системе постановке. Тогда искомое соотношение коэффициентов динамичности 
.
Проведем вычисления в двухмассовой системе.
Решаем задачу о собственных колебаниях при следующих начальных условиях
.
Решение с учетом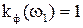 
, 
ищем в виде
,
Из граничных условий
, 
.
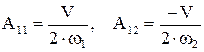Соответственно
.
Численное исследование дает 
.
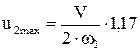После подстановки значения 
получаем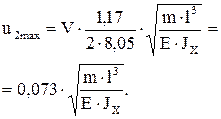 
Окончательно 
.
Расчет удара в одномассовой системе ведется с запасом. В нашем случае запас 23%.
Итак, даже при n=2 невозможно избежать численного решения части задачи. При n>2 целесообразно вообще решать задачу численно и вообще без всяких упрощений. Необходимо просто проинтегрировать (*) при соответствующих начальных условиях, проследить за перемещением точки удара в первой положительной четверти движения, найти её максимальное перемещение, и, поделив его на соответствующую податливость, вычислить силу удара. Если необходимо, найти динамический коэффициент как отношение силы удара к весу ударяющей массы.
Реализация алгоритма в конкретных случаях – тема спецзадания во втором семестре.
