Решим задачу, пренебрегая влиянием трения на частоты собственных колебаний. Поскольку решается однородная система, то из (*) получаем
,
. (**)
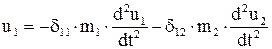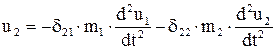Ищем решение в виде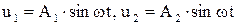 
, и после подстановки в (**), получаем однородную систему линейных уравнений относительно А1,А2
,
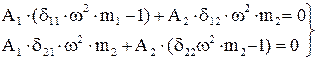ненулевое (нетривиальное) решение которой возможно только при равенстве нулю определителя системы, т.е.
.
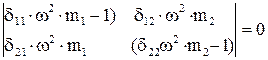Решение в виде косинусов дает тот же результат.
Аналогичное уравнение получается и для системы с n степенями свободы. Однако для двух степеней свободы получает решаемое в квадратурах биквадратное алгебраическое уравнение относительно собственных частот. Его решение –
.
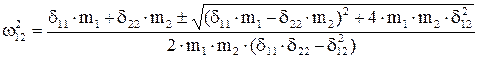Отношение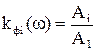 
называют коэффициентом формы собственных колебаний. Для двухмассовой системы это
.
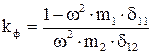Для системы с n степенями свободы решение возможно только численно.
В нашем примере, поделив массу стержня m на две равные части, получаем собственные частоты
, 
, 
.
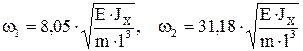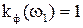Собственные колебания масс по первой частоте синфазные, а по второй - противофазные. Равенство коэффициентов формы единице в примере определяется симметрией задачи.
Заметим для сравнения, что если считать задачу одномассовой с массой посредине, то
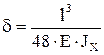и частота собственных колебаний 
.
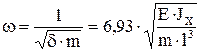Результат иллюстрирует общее свойство собственных частот: низшая частота системы с n степенями свободы всегда несколько больше низшей частоты с меньшим числом степеней свободы.
Для системы с n степенями свободы собственные частоты получаются численным решением уравнения
.
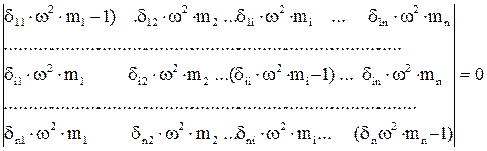В качестве примера рассмотрим результат расчета собственных частот при распределении массы в трех равноудаленных точках:
.
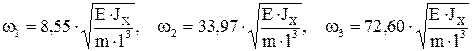Податливости определялись численно и для повышения точности усреднялись: 
и т.д. Как видно, первые две частоты больше, чем определенные для двух степеней свободы. Таким образом, подтверждается правило: расчет по конечномассовой модели всегда дает нижнюю оценку собственных частот.
