Основные определения. В общем случае система m линейных уравнений с n неизвестными имеет следующий вид:

В общем случае система m линейных уравнений с n неизвестными имеет следующий вид:

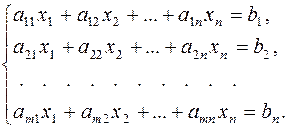(1)

При этом через x ₁, x ₂, …, x_n обозначены неизвестные, подлежащие определению, причем, их число n, не предполагается обязательно равным числу уравнений m. Величины a ₁₁, a ₁₂, …, a_mn, называемые коэффициентами системы, и величины b ₁, b ₂,…, b_n, называемые свободными членами, предполагаются известными.

Решением системы (1) называется такая совокупность n чисел c ₁, c ₂,…, c _n, что каждое из уравнений (1) обращаются в верное числовое равенство после замены в нем неизвестных x_i соответствующими числами c_i, i= 1,2,…, n.

Система уравнений называется совместной, если она имеет, по крайней мере, одно решение, и несовместной, если у нее не существует ни одного решения.

Например, система

является несовместной, ибо в противном случае мы получили бы, что 1=3.

Решить систему уравнений означает найти все её решения или доказать, что она несовместна.

Два решения совместной системы с ₁, с ₂, …, с_n и d ₁, d ₂, …, d_n называют-

ся различными, если нарушается хотя бы одно из равенств с ₁ =d ₁, c ₂ =d ₂, …

…, c_n=d_n.

Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если у нее существуют, по крайней мере, два различных решения.

Система уравнений называется однородной, если свободные члены всех её уравнений равны нулю.

Очевидно, однородная система всегда совместна, ибо обладает решением x ₁ = 0, x ₂ = 0,…, x_n= 0 (т.н. тривиальное решение).

Можно доказать, что, если система уравнений имеет два различных решения, то она имеет бесконечное множество решений.

Справедливость этого наглядно проявляется в случае системы двух уравнений с двумя неизвестными:

(2)

Каждое уравнение системы (2) определяет на плоскости O xy некоторую прямую. Решение системы (2) – это координаты общей точки двух прямых. Но у двух прямых может не существовать общих точек, быть только одна общая точка или бесконечно много общих точек (если прямые совпадают).

Две системы линейных уравнений называются эквивалентными (равносильными), если они или обе несовместимы, или же обе совместны и обладают одними и теми же решениями.