Інфляція стала характерною властивістю економічної дійсності. Знецінення грошей завдає значної шкоди фінансистам, тому інфляцію слід враховувати під час проведення фінансових операцій, особливо довготермінових. Врахування інфляції потрібне хоча б двох випадках: при розрахунках нарощеної суми грошей; при визначенні реальної ставки відсотків.
Виміряти падіння купівельної спроможності грошей статистично, як відомо, можна за допомогою індексу цін Jp (за будь-який проміжок часу) або річного темпу інфляції 
, який показує у відсотках річне підвищення цін.
Якщо нарощена за n років сума грошей становить величину S, а динаміка цін характеризується індексом Jp, що рівнозначне падінню купівельної спроможності грошей в 
разів, то реальна нарощена сума грошей становитиме 
.
Наприклад, якщо за два роки ціни зросли на 50 %, тоді J p=1,5.
Відповідно виплата 200 грн. у цей момент рівнозначна сплаті 
грн. у реальних вимірах.
Нехай протягом n років темп зростання інфляції 
був постійним, тоді за цей час індекс цін становив 
(у скільки разів зросли ціни за n років). Отже, нарощена сума до кінця цього терміну знецінилася у стільки ж разів у зв’язку з інфляцією. Індекс купівельної спроможності грошей набув значення 
. Це означає, що реальна вартість C нарощеної суми S дорівнює
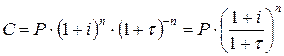(16)
Величина 
– це множник нарощення за складною ставкою відсотків і з урахуванням щорічного темпу інфляції . Як впливають величини і та на цей множник, а відповідно й на нарощену суму?
Якщо річний темп інфляції дорівнює річній ставці відсотків (і= ), то нарощення суми Р поглинатиметься інфляцією, і тоді С=Р, а отже не буде ніякого збільшення суми Р.
Якщо 
, то відбуватиметься “ерозія”, тобто поїдання капіталу і реальна сума грошей через n років буде меншою від початкової суми Р.
Тільки у випадку, коли 
, буде невелике збільшення реальної суми.
Цю залежність реальної суми від і та покажемо графічно (рис. 2).
 |
Рис. 2
У практиці рідко темп інфляції залишається незмінним протягом кількох років. Як правило, він змінюється з кожним роком, тому формула (16) рідко використовується при врахуванні рівня інфляції у фінансових розрахунках.
Фінансисти використовують такі два методи захисту грошей від знецінення: індексацію ставки відсотків і індексацію початкової суми платежу.
Розглянемо перший метод. Позначимо 
складну ставку відсотків, яка враховує інфляцію (ставка-брутто). Тоді, виходячи з принципу фінансової еквівалентності та рівня знецінення грошей за один рік, маємо
.
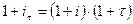Точне значення ставки-брутто –
. (17)
Приклад 11. Банк надає довготерміновий кредит. Ставка відсотків, яка забезпечує нормальний рівень рентабельності для банку, – 10% річних. Однак банк побоюєтеся знецінення грошей, тим більше, що експертна група повідомила про очікуваний середньорічний рівень інфляції за період дії даної кредитної угоди – 8%. Яку ставку треба передбачити у кредитній угоді, щоб застрахувати платежі за користування кредитом від знецінення?
► Дано: і =10%; =8%; -?
За формулою (17)
.
Отже, щоб захистити кредит від знецінення, слід прийняти ставку-брутто 18,8% річних.
Другий метод – індексація початкової суми платежу Р – полягає в тому, що за весь період n задається індекс інфляції Jінф (або індекс Jp). Враховуючи цей індекс, проводять індексацію за формулою
, (18)
де 
- нарощена сума з урахуванням інфляції.
Приклад 12. Визначити нарощену суму з урахуванням інфляції, яка за три роки становила 40%. Початкова сума боргу – 400 тис грн., складна ставка відсотків – 10%. Підвищенню цін на 40% відповідає індекс Jінф =1,4.
► Дано: Р =400000 грн.; і =10%; Jінф =1,4; n =3;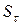 
–?
За формулою (18)
Отже, після індексації грошей нарощена сума боргу через три роки становила 744800 грн. (якби не провели індексації, то S =532000 грн.)
