Формула нарощення боргу за складними відсотками (5) використовується тоді, коли відсоткові гроші нараховуються лише один раз на рік. У практиці частіше буває так, що відсотки нараховуються та капіталізуються не один, а кілька разів на рік – за півріччя, квартали, місяці. Якщо при цьому відсоткова ставка задана на цілий рік, то як обчислити величину одноразової відсоткової ставки?
У контрактах, як правило, фіксується річна сумарна ставка відсотків (позначимо її j) і вказується період нарахування відсотків.
Позначимо m – кількість нарахувань відсотків на рік (m =2; 4; 12;). Тоді, очевидно, кожне нарахування відсотків проводять за ставкою 
. Наприклад, якщо j= 4 %, а відсотки нараховують за півріччя, то кожне нарахування проводять за ставкою 2 %.
Річна сумарна ставка відсотків j при m нарахуваннях відсотків на рік називається номінальною ставкою. Капіталізація відсотків за заданою номінальною ставкою, відбувається за формулою
, (9)
де m×n – кількість нарахувань відсотків за n років; - одноразова ставка відсотків.
Приклад 3. Початкова сума позики – 10000 грн., термін – 4 роки, нарахування складних відсотків на кінець: а) кожного кварталу; б) кожного місяця. Визначити кінцеву суму боргу, якщо номінальна ставка 8% на рік.
► Дано: Р=10000 грн.; n =4; m =4; m =12; j =8% = 0,08; S -?
За формулою (9) маємо:
а)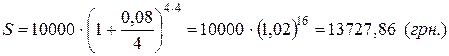 
;
б) 
◄
Знаючи, що процес нарощення складних відсотків відбувається швидше, ніж простих при однакових розмірах відсоткових ставок, з наведеного прикладу можна дійти висновку, що чим частіше нараховуються складні відсотки, тим більша їх сума буде нарахована на початкову суму боргу.
Якщо нараховувати прості відсотки, наприклад, 4 рази на рік за номінальною ставкою 20%, тобто 5% нараховувати поквартально від однієї суми Р, то ця процедура принесе за рік такий же фінансовий результат, що й нарахування 20% раз на рік від суми Р.
Приклад 4. Фінансова угода на 1000 грн. укладена на рік з умовами нарахування відсотків щоквартально за номінальною ставкою 20%; а) простих;
б) складних. Яка кінцева сума боргу?
► Дано: Р =1000 грн.; n =1; m =4; j =20%; S 1 -? S 2 -?
За формулою (5)
За формулою (9)
. ◄
Як бачимо, при різних методах нарахування відсотків (простого і складного) за однаковими параметрами отримали більшу суму відсоткових грошей (I 1 =200 грн.; I 2 =215,5 грн.) при нарахуванні складних відсотків.
Річна ставка складних відсотків, еквівалентна номінальній ставці при нарахуванні відсотків m раз на рік, називається ефективною ставкою, і позначається i або ie. Вона показує реальний відносний дохід, який отримують у цілому за рік.
Еквівалентність ставки ефективності та номінальної ставки означає, що ефективна ставка дає у рік при одноразовому нарахуванні відсотків за нею такий же фінансовий результат, що й m -разове нарахування відсотків на рік за ставкою .
Зрозуміло, що за величиною номінальна ставка та ставка ефективності різні, якщо m> 1. Покажемо взаємозв’язок між цими ставками, використавши принцип фінансової еквівалентності, а з нього – рівність множників нарощення:
– множник нарощення за річною ставкою ефективності;
– множник нарощення за номінальною ставкою.
З рівняння еквівалентності 
випливає рівність
.
Спростивши цю рівність, отримаємо:
формулу ставки ефективності
(10)
формулу номінальної ставки, еквівалентної ефективній ставці
. (11)
Формули (10) і (11) задають зв’язок між двома різними ставками ic та j.
Приклад 5. Банк нараховує на депозити 8% номінальних. Яка реальна доходність вкладів при нарахуванні відсотків: а) за півріччя; б) щоквартально; в) щомісячно; г) щоденно?
► Використавши формулу (10) маємо:
а) 
б) 
в) 
г) 
. ◄
Розрахунки у прикладі 5 доводять, що доходність операції, виміряна ставкою іc, більша від номінальної ставки. Чим більша кількість нарахувань відсотків у рік, тим більша доходність (ефективність) фінансово-кредитної операції.
Приклад 6. Якою повинна бути встановлена номінальна ставка відсотків, що забезпечує річну дохідність на рівні 9%? Нарахування відсотків щомісячне.
► Дано: i =9%; m =12. j -?
За формулою (11) маємо
.
Важливо, що заміна у фінансовій угоді номінальної ставки j при нарахуванні відсотків m раз у рік ефективною ставкою іc, яка визначається за формулою (11), не змінює фінансових зобов’язань обох сторін.
Слід враховувати, що доходність будь-якої фінансово-кредитної операції вимірюється лише ставкою ефективності 
. Саме її можна порівнювати з фінансовими результатами інших капіталовкладень.
