Раніше ми розглядали поняття еквівалентності ставок відсотків і облікових ставок, яка базується на принципі фінансової еквівалентності. Нагадаємо, що цей принцип полягає в тому, що кінцеві фінансові результати не залежать від зміни умов контрактів, зокрема від виду відсоткової ставки, використовуваної у розрахунках.
Розглянемо два види відсоткових ставок: просту 
та складу 
. Нарощення початкової суми за цими ставками здійснюється за формулами:
; (5)
. (6)
Якщо та еквівалентні, то повинен виконуватись принцип фінансової екувівалентності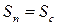 
. Звідси випливає рівність множників нарощення
,
з якої знаходимо:
Ставку простих відсотків, еквівалентну складній ставці відсотків
; (7)
Ставку складних відсотків, еквівалентну простій ставці відсотків
. (8)
Приклад 2. Кредит видали під 8% складних річних. Якою повинна бути еквівалентна ставка простих відсотків при терміні кредиту: а) 10 років; б) 8 місяців?
► За формулою (7) знаходимо:
а) 
;
б) 
.
Отже, для терміну 10 рокі еквівалентні чставки 
, 
; для терміну 8 місяців – 
, . ◄
Як бачимо розмір еквівалентних ставок залежить від терміну користування грошимо.
Графічно процес нарощення за складними та простими відсотками зображено на рис. 1.
Рис. 1
З наведеного прикладу та графікку можна зробити висновок: прості відсотки вигідні кредитору при наданні короткотермінових позичок, а складні – при наданні довготермінових позичок. Відомий один історичний приклад, який ілюструє зміну вартості грошей з часом за складними відсотками.
Острів Матхеттен, на якому розташований Нью-Йорк, куплений у 1624 р. в індійського вождя за 24 дол. Через 350 років вартість землі оцінювалася близько 40 млрд. дол., при цьому використовувалася при розрахунках складна ставка – 6,3%.
