Пользуясь полученными выше результатами, можно найти соотношения между колебаниями тока и напряжения в любой цепи. Рассмотрим последовательное соединение резистора, конденсатора и катушки индуктивности (рис. 8.).
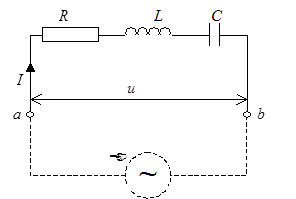 Рис.8. Последовательное соединение резистора, конденсатора и катушки индуктивности
Рис.8. Последовательное соединение резистора, конденсатора и катушки индуктивности
|  Рис.9. Векторная диаграмма
Рис.9. Векторная диаграмма
|
Положим по-прежнему, что ток в цепи изменяется по закону
 ,
,
и вычислим напряжение между концами цепи u. Так как при последовательном соединении проводников складываются напряжения, то искомое напряжение u есть сумма трех напряжений: на сопротивлении 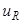 , на емкости
, на емкости  и на индуктивности
и на индуктивности  , причем каждое из этих напряжений, как мы видели, изменяется со временем по закону косинуса:
, причем каждое из этих напряжений, как мы видели, изменяется со временем по закону косинуса:
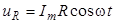 , (5)
, (5)
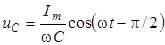 , (6)
, (6)
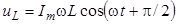 . (7)
. (7)
Для сложения этих трех колебаний воспользуемся векторной диаграммой напряжений. Колебания напряжения на сопротивлении изображаются на ней вектором 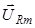 , направленным вдоль оси токов и имеющим длину
, направленным вдоль оси токов и имеющим длину 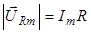 , колебания же напряжений на емкости и индуктивности - векторами
, колебания же напряжений на емкости и индуктивности - векторами 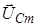 и
и 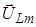 , перпендикулярными к оси токов, с длинами (I m/w C) и (I mw L) (рис.9.). Представим себе, что эти векторы вращаются против часовой стрелки вокруг общего начала с угловой скоростью w. Тогда проекции на ось токов векторов
, перпендикулярными к оси токов, с длинами (I m/w C) и (I mw L) (рис.9.). Представим себе, что эти векторы вращаются против часовой стрелки вокруг общего начала с угловой скоростью w. Тогда проекции на ось токов векторов 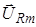 ,
, 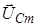 и
и 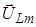 , будут описываться соответственно формулами (5)-(7). Очевидно, что проекция на ось токов суммарного вектора
, будут описываться соответственно формулами (5)-(7). Очевидно, что проекция на ось токов суммарного вектора
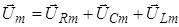
равна сумме  , то есть равна общему напряжению на участке цепи. Максимальное значение этого напряжения равно модулю вектора
, то есть равна общему напряжению на участке цепи. Максимальное значение этого напряжения равно модулю вектора  . Эта величина легко определяется геометрически. Сначала целесообразно найти модуль вектора
. Эта величина легко определяется геометрически. Сначала целесообразно найти модуль вектора  :
:
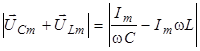 ,
,
а затем по теореме Пифагора:
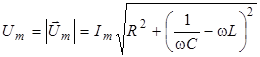 . (8)
. (8)
Из рисунка также видно, что
 . (9)
. (9)
Для напряжения на участке цепи можно записать
 ,
,
где амплитуда напряжения и фазовый сдвиг между током и напряжением определяются формулами (8), (9). Если 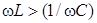 , то напряжение по фазе опережает ток, в противном случае - напряжение отстает по фазе.
, то напряжение по фазе опережает ток, в противном случае - напряжение отстает по фазе.
Формула (8) имеет сходство с законом Ома в том смысле, что амплитуда напряжения пропорциональна амплитуде тока. Поэтому ее иногда называют законом Ома для переменного тока. Однако нужно помнить, что эта формула относится только к амплитудам, но не к мгновенным значениям 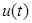 и
и 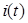 . Величину
. Величину

называют сопротивлением цепи для переменного тока, величину
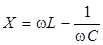
называют реактивным сопротивлением цепи, а величину R - активным сопротивлением.
Полученные формулы справедливы и для замкнутой цепи, включающей в себя генератор переменного напряжения, если под R, C и L понимать их значения для всей цепи (например R представляет собой суммарное активное сопротивление цепи, включая и внутреннее сопротивление генератора). В этом случае во всех формулах следует заменить u на ЭДС генератора. Действительно, для всех наших рассуждений было безразлично, в каком именно месте сосредоточены емкость, индуктивность и сопротивление, поэтому в замкнутой цепи (рис.8) мы можем считать, что 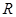 представляет собой суммарное активное сопротивление цепи, включая и внутреннее сопротивление генератора, а
представляет собой суммарное активное сопротивление цепи, включая и внутреннее сопротивление генератора, а 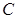 и
и  - емкость и индуктивность цепи, и заменить реальный генератор воображаемым, у которого внутреннее сопротивление равно нулю. При этом напряжение u между точками a и b будет равно ЭДС генератора
- емкость и индуктивность цепи, и заменить реальный генератор воображаемым, у которого внутреннее сопротивление равно нулю. При этом напряжение u между точками a и b будет равно ЭДС генератора 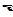 . Отсюда следует, что формулы (8), (9) справедливы и для замкнутой цепи переменного тока, если под
. Отсюда следует, что формулы (8), (9) справедливы и для замкнутой цепи переменного тока, если под 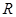 ,
, 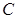 , и
, и  понимать их значения для всей цепи и заменить во всех формулах u на ЭДС генератора
понимать их значения для всей цепи и заменить во всех формулах u на ЭДС генератора  .
.






