Рассмотрим сначала частный случай, когда генератор переменного тока замкнут на внешнюю цепь, имеющую настолько малые индуктивность и емкость, что ими можно пренебречь. Предположим, что в цепи имеется переменный ток
,
(i - мгновенное значение силы тока, 
- амплитуда тока, 
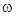- циклическая частота) и найдем, по какому закону изменяется напряжение между концами цепи а и b (рис.1). Применяя к участку аRb закон Ома, получим
.
Таким образом, напряжение на концах участка цепи зависит от времени также по закону косинуса, причем разность фаз между колебаниями тока и напряжения равна нулю (их колебания происходят синфазно): напряжение и ток одновременно достигают максимальных значений и одновременно обращаются в нуль (рис.2). Максимальное значение напряжения есть
.
Рис.1. Резистор в цепи переменного тока
|  Рис.2. Зависимости тока через резистор
и напряжения от времени
|
Рассмотрим теперь, чему равна работа, совершаемая в цепи. В течение малого промежутка времени переменный ток можно рассматривать как постоянный, и поэтому мгновенная мощность переменного тока
.
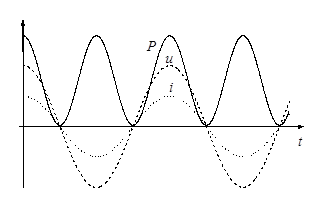
Рис.3. Зависимости тока через резистор, напряжения и мгновенной мощности от времени
Изменение мгновенной мощности с течением времени изображено на рис.3. Здесь же даны кривые колебаний тока i и напряжения u. Обычно необходимо знать не мгновенное значение мощности, а ее среднее значение за большой промежуток времени, охватывающий много периодов колебаний. Так как мы имеем дело с периодическим процессом, то для нахождения этого среднего значения достаточно, очевидно, вычислить среднее значение мощности за один полный период. Работа переменного тока за малое время dt есть
,
а, следовательно, работа A за время полного периода колебаний T выражается формулой
.
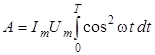Но
.
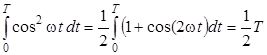Поэтому 
. Отсюда для средней мощности получаем
.
Так как 
, то можно также записать
.
Обозначим через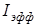 
и 
силу тока и напряжение постоянного тока, который выделяет в сопротивлении R то же количество теплоты, что и данный переменный ток. Тогда
.
Сравнивая эти выражения с выражениями для мощности переменного тока, имеем
.
Величина 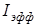называется эффективным значением силы переменного тока, а - эффективным значением напряжения. Пользуясь эффективными значениями, можно выразить среднюю мощность переменного тока теми же формулами, что и мощность постоянного тока.
