В практике создания и использования имитационных моделей весьма часто приходится сталкиваться с необходимостью моделирования важнейшего класса факторов — случайных величин (СВ) различных типов.
Случайной называют переменную величину, которая в результате испытания принимает то или иное значение, причем заранее неизвестно, какое именно. При этом под испытанием понимают реализацию некоторого (вполне определенного) комплекса условий.
В зависимости от множества возможных значений различают три типа СВ: непрерывные, дискретные, смешанного типа.
Исчерпывающей характеристикой любой СВ является ее закон распределения, который может быть задан в различных формах: функции распределения — для всех типов СВ; плотности вероятности (распределения) — для непрерывных СВ; таблицы или ряда распределения — для дискретных СВ.
В данном подразделе изложены основные методы моделирования СВ первых двух типов как наиболее часто встречающихся на практике.
Моделирование непрерывных случайных величин. Моделирование СВ заключается в определении («розыгрыше») в нужный по ходу имитации момент времени конкретного значения СВ в соответствии с требуемым (заданным) законом распределения.
Наибольшее распространение получили три метода: метод обратной функции, метод исключения (фон Неймана), метод композиций.
Метод обратной функции. Метод позволяет при моделировании СВ учесть все ее статистические свойства и основан на следующей теореме.
Если непрерывная СВ Y имеет плотность вероятности f (у), то СВ X, определяемая преобразованием

имеет равномерный закон распределения на интервале [0; 1].
Данную теорему поясняет рис. 10.10, на котором изображена функция распределения СВ Y. Теорему доказывает цепочка рассуждений, основанная на определении понятия «функция распределения» и условии теоремы


Таким образом, получили равенство

а это и означает, что СВ X распределена равномерно в интервале [0; 1].
Напомним, что в общем виде функция распределения равномерно распределенной на интервале [ а; b ]СВ X имеет вид

Теперь можно попытаться найти обратное преобразование функции распределения F( -1 ) (x).
Если такое преобразование существует (условием этого является наличие первой производной у функции распределения), алгоритм метода включает всего два шага:
· моделирование ПСЧ, равномерно распределенного на интервале [0; 1];
· подстановка этого ПСЧ в обратную функцию и вычисление значения СВ Y

При необходимости эти два шага повторяются столько раз, сколько возможных значений СВ Y требуется получить.
Пример. Длина свободного пробега нейтрона в однородном веществе d (d > 0)имеет следующее распределение [18, 35]:

где σ d — среднее квадратическое отклонение длины пробега.
Тогда формула для генерации возможного значения СВ D имеет вид
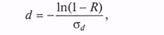
где R — ПСЧ, распределенное равномерно в интервале [0; 1].
Простота метода обратной функции позволяет сформулировать такой вывод: если обратное преобразование функции распределения СВ, возможные значения которой необходимо получить, существует, следует использовать именно этот метод. К сожалению, круг СВ с функциями распределения, допускающими обратное преобразование, не столь широк, что потребовало разработки иных методов.
Метод исключения (фон Неймана). Метод фон Неймана позволяет из совокупности равномерно распределенных ПСЧ Ri, по определенным правилам выбрать совокупность значений уi стребуемой функцией распределения f (у) [18, 35].
Алгоритм метода следующий.
1. Выполняется усечение исходного распределения таким образом, чтобы область возможность значений СВ Y совпадала с интервалом [а; b].
В результате формируется плотность вероятности f *(у) такая, что

Длина интервала [а; b] определяется требуемой точностью моделирования значений СВ в рамках конкретного исследования.
2. Генерируется пара ПСЧ R 1и R 2, равномерно распределенных на интервале [0; 1].
3. Вычисляется пара ПСЧ R 1* и R2 по формулам

где

На координатной плоскости пара чисел (R 1*; R 2 *) определяет точку — например, точку Q 1 на рис. 10.11.

4. Если точка (Q 1) принадлежит области D, считают, что получено первое требуемое значение СВ y 1 = R 1 *.
5. Генерируется следующая пара ПСЧ R 3и R 4, равномерно распределенных на интервале [0; 1], после пересчета по п. 3 задающих на координатной плоскости вторую точку — Q 2.
6. Если точка (Q2) принадлежит области В, переходят к моделированию следующей пары ПСЧ (R 5; R 6 ) и далее до получения необходимого количества ПСЧ.
Очевидно, что в ряде случаев (при попадании изображающих точек в область В соответствующие ПСЧ с нечетными индексами не могут быть включены в требуемую выборку возможных значений моделируемой СВ, причем это будет происходить тем чаще, чем сильнее график f *(у) по форме будет «отличаться» от прямоугольника А. Оценить среднее относительное число q «пустых» обращений к генератору ПСЧ можно геометрическим методом, вычислив отношение площадей соответствующих областей (В и А):

На рис. 10.12 [27] показаны две функции плотности вероятности, вписанные в прямоугольники А и В соответственно. Первая функция соответствует β-распределению с параметрами η = λ = 2. Вторая функция соответствует γ-распределению с параметрами λ = 0,5; σ = 1.

Для первой функции q ≈ 0,33; для второй — q ≈ 0,92. Таким образом, для β-распределения метод фон Неймана почти в три раза эффективнее, чем для γ-распределения. В целом для многих законов распределения (особенно для островершинных и имеющих длинные «хвосты») метод исключения приводит к большим затратам машинного времени на генерацию требуемого количества ПСЧ.
Главным достоинством метода фон Неймана является его универсальность — применимость для генерации СВ, имеющих любую вычислимую или заданную таблично плотность вероятности.
Метод композиции. Применение метода основано на теоремах теории вероятностей, доказывающих представимость одной СВ композицией двух или более СВ, имеющих относительно простые, более легко реализуемые законы распределения. Наиболее часто данным методом пользуются для генерации ПСЧ, имеющих нормальное распределение. Согласно центральной предельной теореме, распределение СВ Y, задаваемой преобразованием
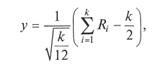
где Ri — равномерно распределенные на интервале [0; 1] ПСЧ, при росте k неограниченно приближается к нормальному распределению со стандартными параметрами (ту = 0; σ = 1).
Последнее обстоятельство легко подтверждается следующим образом. Введем СВ Z инайдем параметры ее распределения, используя соответствующие теоремы о математическом ожидании и дисперсии суммы СВ:
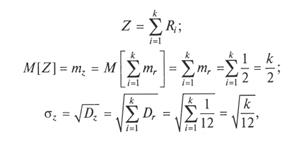
где т — математическое ожидание; r — значение случайных чисел.
При равномерном распределении в интервале [0; 1] СВ имеет параметры: тr = 1/2; Dr = 1/12.
Очевидно, что

и, как любая центрированно-нормированная СВ, имеет стандартные параметры.
Как правило, берут k = 12 и считают, что для подавляющего числа практических задач обеспечивается должная точность вычислений. Если же к точности имитации предъявляются особые требования, можно улучшить качество моделирования СВ за счет введения нелинейной поправки [8]:

где у (k) — возможное значение СВ Y, полученное в результате сложения, центрирования и нормирования k равномерно распределенных ПСЧ Ri.
Еще одним распространенным вариантом применения метода композиции является моделирование возможных значений СВ, обладающей χ2 распределением с п степенями свободы: для этого нужно сложить «квадраты» п независимых нормально распределенных СВ со стандартными параметрами.
Возможные значения СВ, подчиненной закону распределения Симпсона (широко применяемого, например, в радиоэлектронике), моделируют, используя основную формулу метода при k = 2. Существуют и другие приложения этого метода.
В целом можно сделать вывод о том, что метод композиции применим и дает хорошие результаты тогда, когда из теории вероятностей известно, композиция каких легко моделируемых СВ позволяет получить СВ с требуемым законом распределения.
Моделирование дискретных случайных величин. Дискретные СВ (ДСВ) достаточно часто используются при моделировании систем. Основными методами генерации возможных значений ДСВ являются: метод последовательных сравнений, метод интерпретации.
Метод последовательных сравнений. Алгоритм метода практически совпадает с ранее рассмотренным алгоритмом моделирования полной группы несовместных случайных событий, если считать номер события номером возможного значения ДСВ, а вероятность наступления события — вероятностью принятия ДСВ этого возможного значения. На рис. 10.13 показана схема определения номера возможного значения ДСВ, полученного на очередном шаге.

Из анализа ситуации, показанной на рис. 10.13, для ПСЧ R, «попавшего» в интервал [Р 1; Р 1 + Р 2 ], следует сделать вывод, что ДСВ приняла свое второе возможное значение; а для ПСЧ R' — что ДСВ приняла свое (N - 1)-е значение и т.д. Алгоритм последовательных сравнений можно улучшить (ускорить) за счет применения методов оптимизации перебора — дихотомии (метода половинного деления); перебора с предварительным ранжированием вероятностей возможных значений по убыванию и т. п.
Метод интерпретации. Метод основан на использовании модельных аналогий с сущностью физических явлений, описываемых моделируемыми законами распределения.
На практике метод чаще всего используют для моделирования биномиального закона распределения, описывающего число успехов в п независимых опытах с вероятностью успеха в каждом испытании р и вероятностью неудачи q = 1 - р. Алгоритм метода для этого случая весьма прост:
· моделируют п равномерно распределенных на интервале [0; 1] ПСЧ;
· подсчитывают число т тех из ПСЧ, которые меньше р;
· это число т считают возможным значением моделируемой ДСВ, подчиненной биномиальному закону распределения.
Помимо перечисленных, существуют и другие методы моделирования ДСВ, основанные на специальных свойствах моделируемых распределений или на связи между распределениями [7].






