Моделирование случайных векторов

Случайным вектором (системой случайных величин) называют совокупность случайных величин, совместно характеризующих какое-либо случайное явление

 

 

где X_i — СВ с теми или иными законами распределения.

Данный подпункт содержит материал по методам моделирования непрерывных случайных векторов (все компоненты которых представляют собой непрерывные СВ).

Исчерпывающей характеристикой случайного вектора является совместная многомерная функция распределения его компонент F(x ₁, х ₂,..., x_n) или соответствующая ему совместная многомерная плотность вероятности

 

 

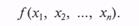
Проще всего моделировать случайный вектор с независимыми компонентами, для которого справедливо

 

 

т.е. каждую из компонент случайного вектора можно моделировать независимо от других в соответствии с ее «собственной» плотностью вероятности f_i (x_i).

В случае, когда компоненты случайного вектора статистически зависимы, необходимо использовать специальные методы: условных распределений, исключения (фон Неймана), линейных преобразований.

Метод условных распределений. Метод основан на рекуррентном вычислении условных плотностей вероятностей для каждой из компонент случайного вектора х с многомерной совместной плотностью вероятности f (x ₁, х ₂, …, x_n).

Для плотности распределения случайного вектора х можно записать:

 

 

где f ₁(x ₁) — плотность распределения СВ X ₁, f_n(x_n/x_{n -1}, х_n-2, …, x ₁) — плотность условного распределения СВ Х_n при условии: Х ₁ = х ₁; Х₂ = x ₂; …; Х_{п -1} = х_{n -1}.

Для получения указанных плотностей необходимо провести интегрирование совместной плотности распределения случайного вектора в соответствующих пределах:

 

 

Порядок моделирования:

· моделировать значение х ₁* СВ Х ₁по закону f ₁ (x ₁ )

 

 

где Q_j — множество случайных величин x_j,

· моделировать значение х ₂ ^* СВ Х ₂по закону f ₂(х ₂/ х ₁*);

· …;

· моделировать значение x_n * СВ Х_n по закону f_п (х_n/х*_{n- 1}, х*_{n- 2} ,..., х ₁ *).

Тогда вектор (x ₁ *, х ₂*,..., x_n *) и есть реализация искомого случайного вектора X.

Метод условных распределений (как и метод обратной функции для скалярной СВ) позволяет учесть все статистические свойства случайного вектора. Поэтому справедлив вывод: если имеется возможность получить условные плотности распределения f_n (x_n / х_{n- 1}, х_{n- 2},..., х ₁), следует пользоваться именно этим методом.

Метод исключения (фон Неймана). Метод является обобщением уже рассмотренного для СВ метода фон Неймана на случай п переменных. Предполагается, что все компоненты случайного вектора распределены в конечных интервалах x_i [a_i, b_i], i = 1, 2,..., п. Если это не так, необходимо произвести усечение плотности распределения для выполнения данного условия.

Алгоритм метода следующий.

1. Генерируются (n + 1) ПСЧ

 

 

распределенных соответственно на интервалах

 

2. Если выполняется условие

 

 

то вектор

 

и есть искомая реализация случайного вектора.

3. Если данное условие не выполняется, переходят к первому пункту и т.д.

Рис. 10.14 содержит иллюстрацию данного алгоритма для двумерного случая R_f £ f(R ₁, R ₂ ).

 

 

Возврат к п. 1 после «неудачного» моделирования п ПСЧ происходит тогда, когда точка Q окажется выше поверхности, представляющей двумерную плотность вероятности f(x ₁, x ₂). Для случая, представленного на рисунке, в качестве (очередной) реализации двумерного случайного вектора следует взять пару ПСЧ (R ₁, R ₂ ).

Среднюю относительную частоту «неудач» можно вычислить геометрическим способом, взяв отношение объемов соответствующих фигур.

Как уже отмечалось для одномерного случая, основным достоинством метода фон Неймана является его универсальность. Однако для плотностей вероятностей, поверхности которых имеют острые пики, достаточно часто будут встречаться «пустые» прогоны, когда очередные п ПСЧ бракуются. Этот недостаток тем существеннее, чем больше размерность моделируемого вектора (п) и длиннее требуемая выборка реализаций случайного вектора. На практике такие ситуации встречаются не слишком часто, поэтому метод исключений и имеет столь широкое распространение.

Метод линейных преобразований. Метод линейных преобразований является одним из наиболее распространенных так называемых корреляционных методов, применяемых в случаях, когда при моделировании непрерывного n -мерного случайного вектора достаточно обеспечить лишь требуемые значения элементов корреляционной матрицы этого вектора (это особенно важно для случая нормального распределения, для которого выполнение названного требования означает выполнение достаточного условия полного статистического соответствия теоретического и моделируемого распределений). Идея метода заключается в линейном преобразовании случайного n -мерного вектора Y cнезависимыми (чаще всего нормально распределенными) компонентами в случайный вектор X с требуемыми корреляционной матрицей и вектором математических ожиданий компонент.

Математическая постановка задачи выглядит следующим образом. Даны корреляционная матрица и математическое ожидание вектора X

 

 

Требуется найти такую матрицу В, которая позволяла бы в результате преобразования

 

 

где Y — n -мерный вектор с независимыми нормально распределенными компонентами со стандартными параметрами, получить вектор Х стребуемыми характеристиками.

Будем искать матрицу В в виде нижней треугольной матрицы, все элементы которой, расположенные выше главной диагонали, равны 0. Перейдем от матричной записи к системе алгебраических уравнений:

 

 

 

Поскольку компоненты вектора у независимы и имеют стандартные параметры, справедливо выражение

 

 

Почленно перемножив сами на себя и между собой соответственно левые и правые части уравнений системы (3.2) и взяв от результатов перемножения математическое ожидание, получим систему уравнений вида

 

 

Как легко увидеть, в левых частях полученной системы уравнений — элементы заданной корреляционной матрицы Q, ав правых — элементы искомой матрицы В. Последовательно решая эту систему, получаем формулы для расчета элементов b_ij:

 

Формула для расчета любого элемента матрицы преобразования В имеет вид

 

 

Таким образом, алгоритм метода линейных преобразований весьма прост:

· по заданной корреляционной матрице рассчитывают значения коэффициентов матрицы преобразования В;

· генерируют одну реализацию вектора Y, компоненты которого независимы и распределены нормально со стандартными параметрами;

· полученный вектор подставляют в выражение (3.1) и определяют очередную реализацию вектора X, имеющего заданные корреляционную матрицу и вектор математических ожиданий компонентов;

· при необходимости два предыдущих шага алгоритма повторяют требуемое число раз (до получения нужного количества реализаций вектора X).

В данной главе рассмотрены основные методы генерации ПСЧ, равномерно распределенных на интервале [0; 1], и моделирования случайных событий, величин и векторов, часто используемые в практике имитационных исследований ЭИС. Как правило, все современные программные средства, применяемые для реализации тех или иных имитационных моделей, содержат встроенные генераторы равномерно распределенных ПСЧ, что позволяет исследователю легко моделировать любые случайные факторы.