В предыдущем разделе было дано формальное определение имитационной модели с точки зрения свойств двух ее важнейших операторов: оператора моделирования исхода и оператора оценивания показателя эффективности. Приведем классическое вербальное определение имитационного моделирования и проведем его краткий анализ
По Р.Шеннону (Robert E.Shannon — профессор университета в Хантсвилле, штат Алабама, США), «имитационное моделирование — есть процесс конструирования на ЭВМ модели сложной реальной системы, функционирующей во времени, и постановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить различные стратегии, обеспечивающие функционирование данной системы» [6].
Выделим в этом определении ряд важнейших обстоятельств, учитывая особенности применения метода для исследования ЭИС.
Во-первых, имитационное моделирование предполагает два этапа: конструирование модели на ЭВМ и проведение экспериментов с этой моделью. Каждый из этих этапов предусматривает использование собственных методов. Так, на первом этапе весьма важно грамотно провести информационное обследование, разработку всех видов документации и их реализацию. Второй этап должен предполагать использование методов планирования эксперимента с учетом особенностей машинной имитации.
Во-вторых, в полном соответствии с системными принципами четко выделены две возможные цели имитационных экспериментов:
· либо понять поведение исследуемой системы (о которой по каким-либо причинам было «мало» информации) — потребность в этом часто возникает, например, при создании принципиально новых образцов продукции;
· либо оценить возможные стратегии управления системой, что также очень характерно для решения широкого круга экономико-прикладных задач.
В-третьих, с помощью имитационного моделирования исследуют сложные системы. Понятие «сложность» является субъективным и по сути выражает отношение исследователя к объекту моделирования. Укажем пять признаков «сложности» системы, по которым можно судить о ее принадлежности к такому классу систем:
· наличие большого количества взаимосвязанных и взаимодействующих элементов;
· сложность функции (функций), выполняемой системой;
· возможность разбиения системы на подсистемы (декомпозиции);
· наличие управления (часто имеющего иерархическую структуру), разветвленной информационной сети и интенсивных потоков информации;
· наличие взаимодействия с внешней средой и функционирование в условиях воздействия случайных (неопределенных) факторов.
Очевидно, что некоторые приведенные признаки сами предполагают субъективные суждения. Вместе с тем становится понятным, почему значительное число ЭИС относят к сложным системам и, следовательно, применяют метод имитационного моделирования. Отметим, что последний признак определяет потребность развития методов учета случайных факторов (см. гл. 10), т. е. проведения так называемой стохастической имитации.
В-четвертых, методом имитационного моделирования исследуют системы, функционирующие во времени, что определяет необходимость создания и использования специальных методов (механизмов) управления системным временем.
Наконец, в-пятых, в определении прямо указывается на необходимость использования ЭВМ для реализации имитационных моделей, т.е. проведения машинного эксперимента (машинной имитации), причем в подавляющем большинстве случаев применяются цифровые машины.
Даже столь краткий анализ позволяет сформулировать вывод о целесообразности (а следовательно, и необходимости) использования метода имитационного моделирования для исследования сложных человеко-машинных (эргатических) систем экономического назначения. Особо выделим наиболее характерные обстоятельства применения имитационных моделей [60]:
· если идет процесс познания объекта моделирования;
· если аналитические методы исследования имеются, но составляющие их математические процедуры очень сложны и трудоемки;
· если необходимо осуществить наблюдение за поведением компонентов системы в течение определенного времени;
· если необходимо контролировать протекание процессов в системе путем замедления или ускорения явлений в ходе имитации;
· если особое значение имеет последовательность событий в проектируемых системах и модель используется для предсказания так называемых «узких» мест;
· при подготовке специалистов для приобретения необходимых навыков в эксплуатации новой техники;
· если имитационное моделирование оказывается единственным способом исследований из-за невозможности проведения реальных экспериментов.
До настоящего момента особое внимание в толковании термина «имитационное моделирование системы» было уделено первому слову. Однако не следует упускать из виду, что создание любой (в том числе и имитационной) модели предполагает, что она будет отражать лишь наиболее существенные с точки зрения конкретной решаемой задачи свойства объекта-оригинала. Английский аналог этого термина — systems simulation — при дословном переводе непосредственно указывает на необходимость воспроизводства (симуляции) лишь основных черт реального явления (сравните с термином «симуляция симптомов болезни» из медицинской практики). Важно отметить еще один аспект: создание любой (в том числе и имитационной) модели есть процесс творческий и каждый автор имеет право на собственную версию модели реальной системы. Однако за достаточно длительное время применения метода накоплены определенный опыт и признанные разумными рекомендации, которыми целесообразно руководствоваться при организации имитационных экспериментов.
Укажем ряд основных достоинств и недостатков метода имитационного моделирования [6, 60].
Основные достоинства:
· имитационная модель позволяет в принципе описать моделируемый процесс с большей адекватностью, чем другие;
· имитационная модель обладает известной гибкостью варьирования структуры, алгоритмов и параметров системы;
· применение ЭВМ существенно сокращает продолжительность испытаний по сравнению с натурным экспериментом (если он возможен), а также их стоимость.
Основные недостатки:
· решение, полученное на имитационной модели, всегда носит частный характер, так как оно соответствует фиксированным элементам структуры, алгоритмам поведения и значениям параметров системы;
· большие трудозатраты на создание модели и проведение экспериментов, а также обработку их результатов;
· если использование системы предполагает участие людей при проведении машинного эксперимента, на результаты может оказать влияние так называемый хауторнский эффект (заключающийся в том, что люди, зная (чувствуя), что за ними наблюдают, могут изменить свое обычное поведение).
Итак, само использование термина «имитационное моделирование» предполагает работу с такими ММ, с помощью которых результат исследуемой операции нельзя заранее вычислить или предсказать, поэтому необходим эксперимент (имитация) на модели при заданных исходных данных. В свою очередь, сущность машинной имитации заключается в реализации численного метода проведения на ЭВМ экспериментов с ММ, описывающими поведение сложной системы в течение заданного или формируемого периода времени [5].
Каждая имитационная модель представляет собой комбинацию шести основных составляющих [5, 53]компонентов, переменных, параметров, функциональных зависимостей, ограничений, целевых функций.
Под компонентами понимают составные части, которые при соответствующем объединении образуют систему. Компоненты называют также элементами системы или ее подсистемами. Например, в модели рынка ценных бумаг компонентами могут выступать отделы коммерческого банка (кредитный, операционный и т.д.), ценные бумаги и их виды, доходы, котировка и т.п.
Параметры — это величины, которые исследователь (пользователь модели) может выбирать произвольно, т. е. управлять ими.
В отличие от них переменные могут принимать только значения, определяемые видом данной функции. Так, в выражении для плотности вероятности нормально распределенной случайной величины х
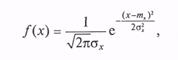
где х — переменная; тх, σх — параметры (математическое ожидание и стандартное отклонение соответственно); π, e — константы.
Различают экзогенные (являющиеся для модели входными и порождаемые вне системы) и эндогенные (возникающие в системе в результате воздействия внутренних причин) переменные. Эндогенные переменные иногда называют переменными состояния.
Функциональные зависимости описывают поведение параметров и переменных в пределах компонента или же выражают соотношения между компонентами системы. Эти соотношения могут быть либо детерминированными, либо стохастическими.
Ограничения — устанавливаемые пределы изменения значений переменных или ограничивающие условия их изменения. Они могут вводиться разработчиком (искусственные) или определяться самой системой вследствие присущих ей свойств (естественные).
Целевая функция предназначена для измерения степени достижения системой желаемой (требуемой) цели и вынесения оценочного суждения по результатам моделирования. Эту функцию также называют функцией критерия. По сути, весь машинный эксперимент с имитационной моделью заключается в поиске таких стратегий управления системой, которые удовлетворяли бы одной из трех концепций ее рационального поведения: оптимизации, пригодности или адаптивизации [26]. Если показатель эффективности системы является скалярным, проблем с формированием критерия не возникает и, как правило, решается оптимизационная задача — поиска стратегии, соответствующей максимуму или минимуму показателя. Сложнее дело обстоит, если приходится использовать векторный показатель. В этом случае для вынесения оценочного суждения используются методы принятия решений по векторному показателю в условиях определенности (когда в модели учитываются только детерминированные факторы) или неопределенности (в противном случае).
При реализации имитационной модели, как правило, рассматриваются не все реально осуществляемые функциональные действия системы (ФД), а только те из них, которые являются наиболее существенными для исследуемой операции. Кроме того, реальные ФД аппроксимируются упрощенными действиями ФД', причем степень этих упрощений определяется уровнем детализации учитываемых в модели факторов. Названные обстоятельства порождают ошибки имитации процесса функционирования реальной системы, что, в свою очередь, обусловливает адекватность модели объекту-оригиналу и достоверность получаемых в ходе моделирования результатов.
На рис. 9.1 схематично представлен пример выполнения некоторых ФД в i -м компоненте реальной системы и ФД ' в i -м компоненте ее модели.
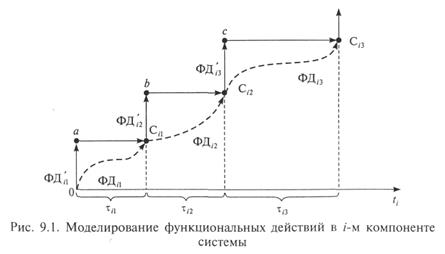
В i -м компоненте реальной системы последовательно выполняются ФД i 1, ФД i 2, ФД i 3), … за время τ i 1, τ i 2, τ i 3, … соответственно. На рисунке эти действия условно изображены пунктирными («непрямыми») стрелками. В результате ФД наступают соответствующие события: С i 1 С i 2, С i 3,.... В модели последовательность имитации иная: выполняется ФД 'i 1 при неизменном времени, наступает модельное событие а, после чего время сдвигается на величину τ i 1 инициируя наступление события С i 1 и т.д. Иными словами, модельной реализации упрощенных ФД (ФД ') соответствует ломаная (0, а, С i 1 b, C i 2, d, С i 3,...). Отметим, что в принципе возможен и другой порядок моделирования: сначала сдвигать время, а затем инициировать наступление соответствующего события.
Очевидно, что в реальной системе в различных ее компонентах могут одновременно (параллельно) производиться функциональные действия и соответственно наступать события. В большинстве же современных ЭВМ в каждый из моментов времени можно отрабатывать лишь один алгоритм какого-либо ФД. Возникает вопрос: каким образом учесть параллельность протекания процессов в реальной системе без потери существенной информации о ней?
Для обеспечения имитации наступления параллельных событий в реальной системе вводят специальную глобальную переменную t 0, которую называют модельным (системным) временем. Именно с помощью этой переменной организуется синхронизация наступления всех событий в модели ЭИС и выполнение алгоритмов функционирования ее компонентов. Принцип такой организации моделирования называется принципом квазипараллелизма [5].
Таким образом, при реализации имитационных моделей используют три представления времени:
· t p— реальное время системы;
· t 0 — модельное (системное) время;
· t м— машинное время имитации.






