В качестве основного классификационного признака для ММ целесообразно использовать свойства операторов моделирования исхода операции и оценивания показателя ее эффективности [12, 35].
Оператор моделирования исхода Н может быть функциональным (т. е. заданным системой аналитических функций) или алгоритмическим (т. е. содержать математические, логические и логико-лингвистические операции, не приводимые к последовательности аналитических функций). Кроме того, он может быть детерминированным (когда каждому элементу множества U ´ Λ соответствует детерминированное подмножество значений выходных характеристик модели  Y или стохастическим (когда каждому значению множества U ´ Λ соответствует случайное подмножество
Y или стохастическим (когда каждому значению множества U ´ Λ соответствует случайное подмножество  ).
).
Оператор, оценивания показатель эффективности ψ, может задавать либо точечно-точечное преобразование (когда каждой точке множества выходных характеристик Y ставится в соответствие единственное значение показателя эффективности W), либо множественно-точечное преобразование (когда показатель эффективности задается на всем множестве полученных в результате моделирования значений выходных характеристик модели).
В зависимости от свойств названных операторов все ММ делятся на три основных класса: аналитические, статистические, имитационные.
Для аналитических моделей характерна детерминированная функциональная связь между элементами множеств U, Λ, Y, а значение показателя эффективности W определяется с помощью точечно-точечного отображения. Аналитические модели имеют весьма широкое распространение. Они хорошо описывают качественный характер (основные тенденции) поведения исследуемых систем. В силу простоты их реализации на ЭВМ и высокой оперативности получения результатов такие модели часто применяются при решении задач синтеза систем, а также при оптимизации вариантов применения в различных операциях.
К статистическим относят ММ систем, у которых связь между элементами множеств U, Λ, Y задается функциональным оператором Н, а оператор ψявляется множественно-точечным отображением, содержащим алгоритмы статистической обработки. Такие модели применяются в тех случаях, когда результат операции является случайным, а конечные функциональные зависимости, связывающие статистические характеристики учитываемых в модели случайных факторов с характеристиками исхода операции, отсутствуют. Причинами случайности исхода операции могут быть случайные внешние воздействия; случайные характеристики внутренних процессов; случайный характер реализации стратегий управления. В статистических моделях сначала формируется представительная выборка значений выходных характеристик модели, а затем производится ее статистическая обработка с целью получения значения скалярного или векторного показателя эффективности.
Имитационными называются ММ систем, у которых оператор моделирования исхода операции задается алгоритмически. Когда этот оператор является стохастическим, а оператор оценивания показателя эффективности задается множественно-точечным отображением, имеем классическую имитационную модель, которую более подробно рассмотрим в гл. 9. Если оператор H является детерминированным, а оператор ψ задает точечно-точечное отображение, можно говорить об определенным образом вырожденной имитационной модели.
На рис. 8.2 представлена классификация наиболее часто встречающихся математических моделей по рассмотренному признаку.

Важно отметить, что при создании аналитических и статистических моделей широко используются их гомоморфные свойства (способность одних и тех же ММ описывать различные по физической природе процессы и явления). Для имитационных моделей в наибольшей степени характерен изоморфизм процессов и структур, т. е. взаимно однозначное соответствие элементов структур и процессов реальной системы элементам ее математического описания и соответственно модели.

Согласно [53], изоморфизм — соответствие (отношение) между объектами, выражающее тождество их структуры (строения). Именно таким образом организовано большее число классических имитационных моделей. Названное свойство имитационных моделей проиллюстрировано рис. 8.3.

Имитационные модели являются наиболее общими ММ. В силу этого иногда все модели называют имитационными [55]:
· аналитические модели, «имитирующие» только физические законы, на которых основано функционирование реальной системы, можно рассматривать как имитационные модели I уровня;
· статистические модели, в которых, кроме того, «имитируются» случайные факторы, можно называть имитационными моделями II уровня;
· собственно имитационные модели, в которых еще имитируется и функционирование системы во времени, называют имитационными моделями III уровня.
Классификацию ММ можно провести и по другим признакам [53].
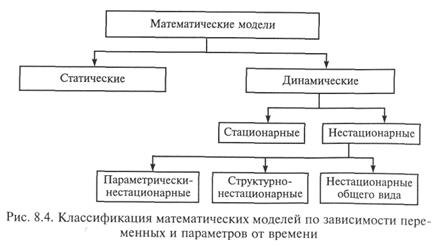
На рис. 8.4 представлена классификация моделей (прежде всего аналитических и статистических) по зависимости переменных и параметров от времени. Динамические модели, в которых учитывается изменение времени, делятся на стационарные (в которых от времени зависят только входные и выходные характеристики) и нестационарные (в которых от времени могут зависеть либо параметры модели, либо ее структура, либо и то, и другое). На рис. 8.5 показана классификация ММ еще по трем основаниям: по характеру изменения переменных; особенностям используемого математического аппарата; способу учета проявления случайностей. Названия типов (видов) моделей в каждом классе достаточно понятны. Укажем лишь, что в сигнально-стохастических моделях случайными являются только внешние воздействия на систему. Имитационные модели, как правило, можно отнести к типам:
· по характеру изменения переменных — к дискретно-непрерывным моделям;
· математическому аппарату — к моделям смешанного типа;
· способу учета случайности — к стохастическим моделям общего вида.