Математическая модель системы

Задача построения математической модели ЭИС может быть поставлена следующим образом [5, 53]: для конкретной цели моделируемой операции с учетом имеющихся ресурсов построить операторы моделирования исхода операции и оценки показателя ее эффективности. Формальная запись этой задачи имеет вид

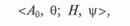
где А ₀ — цель моделируемой операции; θ — ресурсы; Н — оператор моделирования исхода операции; ψ — оператор оценки показателя эффективности операции.

Перед рассмотрением каждого из названных операторов приведем два важных определения.

Оператором в математике называют закон (правило), согласно которому каждому элементу х множества X ставится в соответствие определенный элемент у множества Y. При этом множества Х и Y могут иметь самую различную природу (если они представляют, например, множества действительных или комплексных чисел, понятие «оператор» совпадает с понятием «функция»).

Множество Z упорядоченных пар (х, у), где х Х, y Y, называется прямым произведением множеств Х и Y и обозначается Х ´ Y. Аналогично множество Z упорядоченных конечных последовательностей (x ₁, x ₂ ,..., х_n), где x_k X_k, называется прямым произведением множеств Х ₁, Х ₂ ..., X_N и обозначается Z = X ₁´ X ₂´ ... ´ X_N [5, 12].

Оператором моделирования исхода операции называется оператор H, устанавливающий соответствие между множеством Λ учитываемых в модели факторов, множеством U возможных стратегий управления системой (операцией) и множеством Y значений выходных характеристик модели

где θ_м — ресурсы на этапе моделирования исходов операции; R_s — учитываемые свойства моделируемой системы.

Оператором оценки показателя эффективности системы (операции) называется оператор ψ, ставящий в соответствие множеству Y значений выходных характеристик модели множество W значений показателя эффективности системы

где θ_э — ресурсы исследователя на этапе оценивания эффективности системы.

Особо отметим, что построение приведенных операторов всегда осуществляется с учетом главного системного принципа — принципа цели. Кроме того, важным является влияние объема имеющихся в распоряжении исследователя ресурсов на вид оператора моделирования исхода H и состав множества U стратегий управления системой (операцией). Чем больше выделенные ресурсы, тем детальнее (подробнее) может быть модель и тем большее число стратегий управления может быть рассмотрено (из теории принятия решений известно, что первоначально множество возможных альтернатив должно включать как можно больше стратегий, иначе можно упустить наилучшую).

В самом общем виде математической моделью системы (операции) называется множество

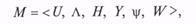
элементами которого являются рассмотренные выше множества и операторы.

Способы задания оператора ψ и подходы к выбору показателя эффективности W рассматриваются в теории эффективности; методы формирования множества возможных альтернатив — в теории принятия решений.

Для двух классов задач показатель эффективности в явном виде не вычисляется [27]:

· для задач «прямой» оценки, в которых в качестве показателей эффективности используются значения одной или нескольких выходных характеристик модели;

· демонстрационных задач, в ходе решения которых для изучения поведения системы используются лишь значения ее выходных характеристик и внутренних переменных.

В таких случаях используют термин «математическое описание системы», представляемое множеством

M' = <U, Λ, H, Y >.