Цели работы:
· Получение навыков построения графиков функций, заданных в различной форме, средствами MathCAD.
Место проведения: аудитория ___.
Ход работы.
1. Для построения графиков в пакете MathCAD существуют встроенные функции пользователя для вызова графиков различного типа (декартова система координат (двух- и трехмерная), полярная система и т.д.). Соответствующие встроенные функции находятся на панели инструментов: \ Вид \ Панели инструментов \ График.
Для наших целей выбираем двухмерную декартову систему координат.
Пусть у нас есть функция fl(X), где X меняется от 0 до 3.5 с шагом 0.1
Заполняем нижнее поле ввода: X, vx; верхнее поле: fl(X), vy и получаем:
Теперь следует определить пределы изменения по оси X и Y. По оси X: min(vx)-0.1 и max(vx)+0.1; по оси Y: min(vy)-2 и max(vy)+2. Получаем:
Как видим, графики практически совпали. Значения
vy заданы в виде 10 точек, поэтому хотелось бы изобразить их отдельными точками. Для этого установим курсор мыши на выделенном графике и вызовем контекстное меню (щелчком правой кнопки мыши). В контекстном меню выберем «Формат…». Получим диалоговое окно «Формат», в котором открываем вторую закладку «След» (рис. 2). В первом столбце таблицы на этой закладке указан номер изображаемой линии. Во втором – символ, которым эта линия изображается (нет символа, крестики и т.п.). В третьем – вид линии (сплошная, пунктирная и т.п.). В четвертом – цвет линии. В пятом – тип линии (линией, точками и т.д.). В последнем столбце указывается толщина линии в пунктах.
 .
.
Рис. 2
У нас график vy задан вторым, поэтому установим настройки для второй линии, как указано на рис. 2, и получим:
Задание 1: Постройте графики функций, заданных в явной, неявной и параметрической форме. Запишите уравнения касательной и нормали к каждой кривой в указанных точках и изобразите их на графике.
Варианты индивидуальных заданий 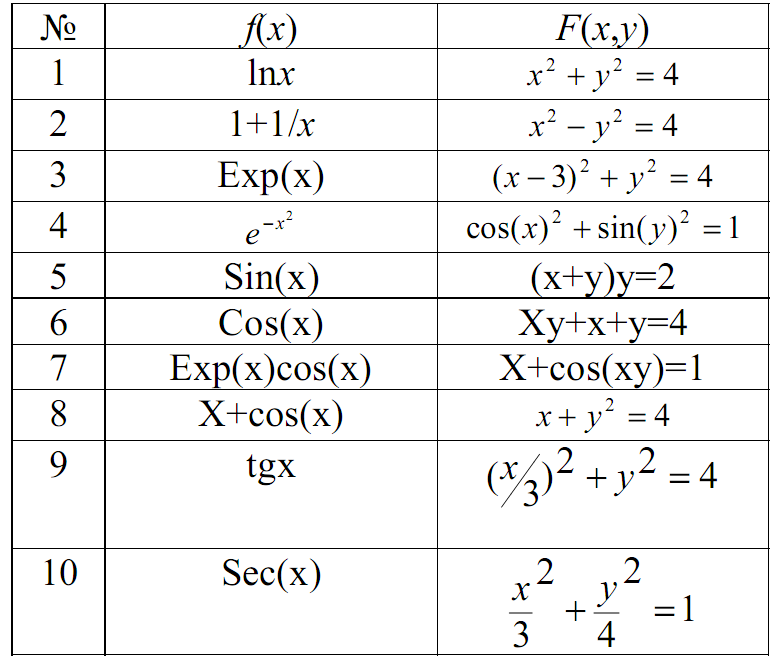
Литература:
1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича.
2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил.
3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000.
4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с.
5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
ЛАБОРАТОРНО – ПРАКТИЧЕСКАЯ РАБОТА 4.


 .
.