1. Строим оси координат;
2. Отмечаем А(1; 0) – первую точку интегральной кривой;
3. Ищем угол наклона касательной к графику в точке A:



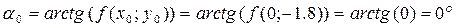
4. Строим касательную l0 в точке А под углом α0;
5. Находим х1 по формуле: xi = х0 + ih, где h – шаг интегрирования
x1 = 0 + 1 · 0,2 = 1,2;
6. Отмечаем середину отрезка x0x1: x0 + h/2, проводим прямую из этой точки до прямой l0, отмечаем точку B(xB; yB);
7. Ищем координаты В:
xB = x0 + h/2 = 0 + 0,2/2 = 0.1
yB = y0 + h/2 · f(x0; y0) = -1.8 + 0,2/2 · 0 = -1.8
Следовательно, точка B имеет координаты (0.1; -1,8);
8. Ищем угол наклона касательной к графику в точке B:
αB = arctg(f(xB; yB)) = arctg((0.1 –(-1.8)2+2*0.1*(-1.8)) = arctg(-0.036) = 2°
9. Строим касательную l1 в точке B под углом αB;
10. Проводим прямую x = x1 = 1,2 до пересечения с прямой l1, отмечаем точку C(x1; y1);
11. Ищем y точки C:
y1 = yB + h/2(f(xB;yB)) = -1.8+ 0,2/2 · (-0.036) = -1.8036
Следовательно, точка C имеет координаты (1,2; -1.8036).
Алгоритм решения задачи.
Алгоритм функции.
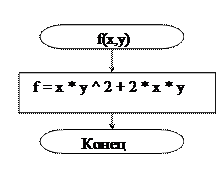 |
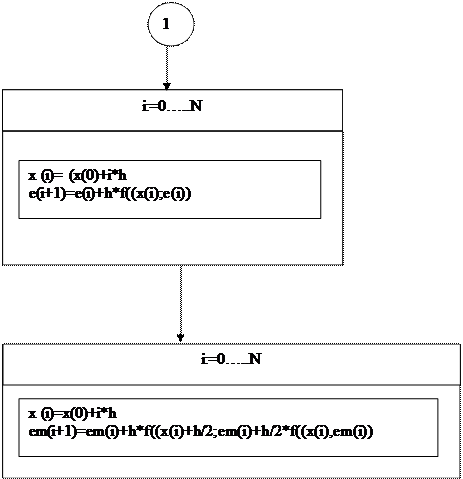
Алгоритм программы.
 |
 | ||||||
 | ||||||
 | ||||||
 |
 |
| |||||
 | |||||
 |
Форма программы.
 |













Листинг программы.
Private x() As Single, e() As Single, em() As Single, o() As Single, y() As Single
Private i, n As Integer
Private x0, xk, y0, h, miny, maxy, minx, maxx As Single
Function f(x, y) As Single
' Сама функция
f = x * y ^ 2 + 2 * x * y
End Function
Private Sub Eiler()
ReDim x(n)
ReDim e(n)
x(0) = x0
e(0) = y0
For i = 0 To n - 1
x(i) = Round(x0 + (i * h), 3)
e(i + 1) = Round(e(i) + h * f(x(i), e(i)), 3)
Next i
End Sub
Private Sub EilerM()
ReDim x(n)
ReDim em(n)
x(0) = x0
em(0) = y0
For i = 0 To n - 1
x(i) = Round(x0 + i * h, 3)
em(i + 1) = Round(em(i) + h * f(x(i) + h / 2, em(i) + h / 2 * f(x(i), em(i))), 3)
Next i
End Sub
Private Sub Obshee()
ReDim x(n)
ReDim o(n)
x(0) = x0
o(0) = y0
' maxy = y0
' miny = y0
' maxx = x0
' minx = x0
For i = 1 To n
x(i) = Round(x0 + i * h, 3)
' If x(i) > maxx Then maxx = x(i)
' If x(i) > maxx Then maxx = x(i)
o(i - 1) = (-2) / (1 + f(x(i), o(i)) * (Exp(-x(i)) ^ 2))
o(i) = Round(ft * (x(i) - 1), 3)
Next i
End Sub
Private Sub Command1_Click()
x0 = Val(Text1.Text)
xk = Val(Text2.Text)
h = Val(Text3.Text)
y0 = Val(Text4.Text)
n = Round((xk - x0) / h)
ReDim x(n)
ReDim e(n)
ReDim em(n)
ReDim o(n)
' Готовим таблицу
MSFlexGrid1.Cols = 4
MSFlexGrid1.Rows = n + 2
MSFlexGrid1.TextMatrix(0, 0) = "x"
MSFlexGrid1.TextMatrix(0, 1) = "Общее рещение"
MSFlexGrid1.TextMatrix(0, 2) = "эйлер"
MSFlexGrid1.TextMatrix(0, 3) = "Эйлер модиф."
Eiler
EilerM
Obshee
For i = 0 To n ' Заполняем таблицу
MSFlexGrid1.TextMatrix(i + 1, 0) = Str(x(i))
MSFlexGrid1.TextMatrix(i + 1, 1) = Str(o(i))
MSFlexGrid1.TextMatrix(i + 1, 2) = Str(e(i))
MSFlexGrid1.TextMatrix(i + 1, 3) = Str(em(i))
Next i
minx = x(0)
maxx = x(n)
' miny =
' maxy = 1
For i = 0 To n
If miny > o(i) Then miny = o(i)
If miny > e(i) Then miny = e(i)
If miny > em(i) Then miny = em(i)
If maxy < o(i) Then maxy = o(i)
If maxy < e(i) Then maxy = e(i)
If maxy < em(i) Then maxy = em(i)
Next i
If miny = maxy Then
miny = -2
maxy = 2
End If
' Находим верхнюю границу граффика
If e(n) > o(n) Then maxy = e(n)
If em(n) > o(n) Then maxy = em(n)
If e(n) > em(n) Then maxy = e(n)
Picture1.Cls
Label10.Caption = Str(miny)
Label11.Caption = Str(maxy)
Label8.Caption = Str(minx)
Label12.Caption = Str(maxx)
' пытаемся найти правильный маштаб
kx = (Picture1.Width - 1200) / (maxx - minx)
ky = (Picture1.Height - 1200) / Abs(maxy - miny)
For i = 0 To n - 1 ' Рисуем Эйлер
z1 = Round(600 + (x(i) - x0) * kx)
z2 = Round(6480 - (e(i) - miny) * ky)
z3 = Round(600 + (x(i + 1) - x0) * kx)
z4 = Round(6480 - (e(i + 1) - miny) * ky)
Picture1.Line (z1, z2)-(z3, z4), RGB(0, 0, 9999)
Next i
For i = 0 To n - 1 ' Рисуем ЭйлерМ
z1 = Round(600 + (x(i) - x0) * kx)
z2 = Round(6480 - (em(i) - miny) * ky)
z3 = Round(600 + (x(i + 1) - x0) * kx)
z4 = Round(6480 - (em(i + 1) - miny) * ky)
Picture1.Line (z1, z2)-(z3, z4), RGB(0, 9999, 0)
Next i
For i = 0 To n - 1 ' Рисуем общее решение
z1 = Round(600 + (x(i) - x0) * kx)
z2 = Round(6480 - (o(i) - miny) * ky)
z3 = Round(600 + (x(i + 1) - x0) * kx)
z4 = Round(6480 - (o(i + 1) - miny) * ky)
Picture1.Line (z1, z2)-(z3, z4), RGB(9999, 0, 0)
Next i
End Sub
Решение задачи в MathCad.


Заключение.
В данной курсовой работе я рассматривала два метода решения дифференциального уравнения, а именно Метод Эйлера и Эйлера модифицированного. Эти методы были рассчитаны путем вычисления через программу Visual Basic и MathCadе.
В связи с полученными данными, вычисленными через программы выяснилось, что точки графиков функции не совпадают, то есть имеется погрешность с каждым увеличением шага или с вычислением последующей точки.
С точки зрения вычислений данного дифференциального уравнения, на мой взгляд, проще решается с помощью метода Эйлера, но при этом возникает небольшая погрешность.






