При разработке технического предложения параллельно синтезу схемы ведут анализ, в процессе которого уточняют значения принимаемых величин, исследуют параметры используемых механизмов, проводят оценку эксплуатационных характеристик машины и т.д.
Исследование установившегося движения насоса.
Обобщенной координатой считаем угол поворота кривошипа АВ. Обобщенную скорость – скорость кривошипа АВ, при установившемся движении определяем из выражения кинетической энергии насоса:
 ; где
; где
 ;
;
а приводной момент инерции:

Значения  и ∆Iпрi= Iнес.прi+Iпоп.прi берем из таблицы 6.3, Т0=36,7016 кДж – начальная кинетическая энергия и Iпр* =120,645 кг×м2 - постоянная составляющая момента инерции маховых масс – определены выше.
и ∆Iпрi= Iнес.прi+Iпоп.прi берем из таблицы 6.3, Т0=36,7016 кДж – начальная кинетическая энергия и Iпр* =120,645 кг×м2 - постоянная составляющая момента инерции маховых масс – определены выше.
Результаты вычислений заносим в таблицу 7.1 таблица 7.1
| Положения механизма | |||||||||
| φ100 | |||||||||
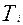 , Дж , Дж
| 36701,6 | 36537,3 | 36356,6 | 36225,1 | 36044,4 | 36340,1 | 36389,4 | 36405,9 | 36432,7 |
| Iпрi, кг×м2 | 122,140 | 122,386 | 121,026 | 120,833 | 123,034 | 122,090 | 121,434 | 121,432 | 120,941 |
| ωi, с-1 | 24,5 | 24,4 | 24,5 | 24,49 | 24,2 | 24,3 | 24,48 | 24,49 | 24,55 |
С помощью таблицы 7.1 проверяем достоверность определения параметров маховика:
ωср=(ωmax+ωmin)/2=(24,55+24,2)/2=24,375 c-1
δ=(ωmax-ωmin)/ωср=(24,55-24,2)/24,375=0,03;
что соответствует принятым значениям
По данным таблицы 7.1 строим график обобщенной скорости станка в функции его обобщенной координаты (ω1=f(φ10)) в пределах одного цикла установившегося движения 0<=φ10<=2π. С помощью этого графика можно определить угловое ускорение кривошипа АВ в любом его положении:
ε = dω/dt = dω/dφ· dφ/dt = ω· dω/dφ = lim∆x→0ω·∆y/∆x·μω/μφ = ω·μω/μφ·tgα;
где:
∆y и ∆x – приращение координат по осям ω1 и φ10; μω и μφ – масштабы этих осей; α- угол касательной и построенной кривой ω1=f(φ10) с положительным направлением оси φ при выбранном значении обобщенной координаты φ10.
Определение реакций в кинематических парах механизма.
Для определения реакций в кинематических парах механизма воспользуемся принципом Д’Аламбера, согласно которому, если ко всем звеньям приложить силы инерции, то движение этих звеньев можно описать уравнениями статики.
Принцип Д’Аламбера применяют к простейшим определимым кинематическим цепям (структурным группам), степень подвижности которых W=0.
Отсоединение указанных цепей ведут от рабочего органа, последовательно приближаясь к валу приводного электродвигателя. В данной работе необходимо рассчитать только несущий механизм.
Исследуем механизм в 3-ом положении
Планы скоростей и ускорений.
ω1 = 24,375 м/с
υА=ω1∙lАВ = 24,375∙0,071=1,73 м/с
Отобразим отрезком pa скорость υА. р—полюс плана скоростей. Тогда масштабный коэффициент μυ=0,04 м/с∙мм, что соответствует рекомендуемым.
Вектор  перпендикулярен к кривошипу при данном расположении и направлен в сторону его вращения. Он представляет собой план скоростей кривошипа АВ.
перпендикулярен к кривошипу при данном расположении и направлен в сторону его вращения. Он представляет собой план скоростей кривошипа АВ.
Переходим к построению плана скоростей для группы ВСD. Скорости точек В и D известны: υА изображена на плане скоростей  , а υD =0. определим скорость точки C. По отношению к точке B уравнение в векторном виде можно записать как
, а υD =0. определим скорость точки C. По отношению к точке B уравнение в векторном виде можно записать как 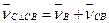 (1). По отношению к точке D
(1). По отношению к точке D  (2).
(2).
Уравнения (1),(2) решаем графически.
Согласно(1) из точки а проводим прямую перпендикулярную к CB. Согласно(2) при υD =0 из точки р проводим перпендикуляр к CE. Точка пересечения двух перпендикуляров является концом вектора  .
.
Этот вектор изображает абсолютную скорость точки В.
Из чертежа  = 33,64 мм. Тогда υВ=1,35 м/с.
= 33,64 мм. Тогда υВ=1,35 м/с.
Переходим к определению скоростей группы DEF. Точка E принадлежит звену 3`, а точка F принадлежит ползуну 4. Для точек E и F, принадлежащих разным звеньям, записывают векторное уравнение  (3). Из подобия треугольников CDE и pce получаем следующую методику нахождения планов скорости
(3). Из подобия треугольников CDE и pce получаем следующую методику нахождения планов скорости  и
и  : из полюса p проводим прямую, перпендикулярную DE. Из точки b проводим перпендикуляр к линии, соединяющей точки C и E. На пересечении этих двух прямых лежит точка e, вектор которой
: из полюса p проводим прямую, перпендикулярную DE. Из точки b проводим перпендикуляр к линии, соединяющей точки C и E. На пересечении этих двух прямых лежит точка e, вектор которой  и есть план скорости точки E. Из точки e проводим прямую, параллельную DE, а из полюса p – прямую, параллельную оси хх. На пересечении этих двух прямых лежит точка f, а вектор
и есть план скорости точки E. Из точки e проводим прямую, параллельную DE, а из полюса p – прямую, параллельную оси хх. На пересечении этих двух прямых лежит точка f, а вектор  есть план скорости для точки F.
есть план скорости для точки F.
В результате получаем:
υD = 2,77 м/с
Определение ускорений.
Чтобы воспользоваться принципом Д’Аламбера, необходимо найти ускорения центров масс и угловые ускорения. Эту задачу решаем путем построения плана ускорений (см. лист 2).
В расчетном положении рассматриваемой кинематической цепи при установившемся движении станка из таблицы 6.1 находим:
 ,а с помощью графика
,а с помощью графика  определяем
определяем  следовательно
следовательно  и
и  противоположны по направлению.
противоположны по направлению.
По теореме о вращательном движении кривошипа AB, ускорение точки B: 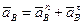 , где нормальная составляющая ускорения
, где нормальная составляющая ускорения 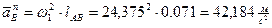 на чертеже (лист 2) отложена в векторе
на чертеже (лист 2) отложена в векторе 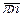 в направлении от точки B кривошипа AB к центру его вращения A, а тангенциальная составляющая
в направлении от точки B кривошипа AB к центру его вращения A, а тангенциальная составляющая  отложена в векторе
отложена в векторе 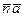 в соответствии с направлением углового ускорения
в соответствии с направлением углового ускорения  перпендикулярно вектору
перпендикулярно вектору 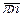 . (
. ( )
)
Ускорение точки C определяется совместным решением векторных уравнений сложного движения точки C относительно точки B:  и вращательного движения точки В:
и вращательного движения точки В:  .
.
Для точки E45, принадлежащей кулисному камню 4 и ползуну – поршню по теореме о сложном движении получаем:

ускорение Кориолиса определяется как  ,
,  - определяется из плана скоростей. Ускорение точки E3 ранее рассматриваемого звена CDE можем найти по теореме о подобии планов ускорений и положений:
- определяется из плана скоростей. Ускорение точки E3 ранее рассматриваемого звена CDE можем найти по теореме о подобии планов ускорений и положений: 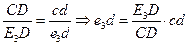 .,
.,
Чтобы определить  и
и  , определим нормальные составляющие ускорений
, определим нормальные составляющие ускорений  ,
, 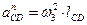 и ускорение Кориолиса
и ускорение Кориолиса 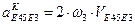 , где
, где
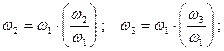
 . Выписав из таблицы 6.2 значения передаточных функций
. Выписав из таблицы 6.2 значения передаточных функций  =0,1084;
=0,1084;  =0,1589, определив по формуле
=0,1589, определив по формуле  ,получаем
,получаем 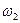 = 2,64с-1
= 2,64с-1 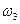 =3,873с-1
=3,873с-1  = 0,428м/с, вследствие чего
= 0,428м/с, вследствие чего  ,
, 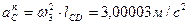 ,
,  =3,315 м/с 2 .
=3,315 м/с 2 .
После графического решения уравнений для  и определения отрезка cd получаем длины отрезков из уравнения для e3d, измерив E3D непосредственно по чертежу.
и определения отрезка cd получаем длины отрезков из уравнения для e3d, измерив E3D непосредственно по чертежу.
При графическом решении вектор ускорения Кориолиса  направлен как вектор скорости
направлен как вектор скорости  , повернутый на 90° в направлении ω3.
, повернутый на 90° в направлении ω3.
Построенный план ускорений используем для определения ускорений центров масс и угловых ускорений звеньев:

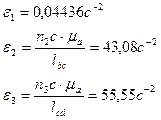
Расчет сил инерции.
Имея ускорения, находим силы инерции:

где  - момент инерции относительно оси вращения О связанных между собой кривошипа АВ и и зубчатого колеса Z5.
- момент инерции относительно оси вращения О связанных между собой кривошипа АВ и и зубчатого колеса Z5.
Определение реакций в кинематических парах.
Прикладываем силы инерции и моменты сил инерции к соответствующим звеньям противоположно ускорениям центров масс и угловым ускорениям этих звеньев. Кроме того, в центрах масс прикладываем силы тяжести звеньев:

К рабочему органу прикладываем силу полезного сопротивления, которая в соответствии с графиком нагрузок в данном положении составляет Fпс=7147 Н. К кривошипу прикладываем “уравновешивающую силу” – действующую на колесо Z5 со стороны колеса Z4 по линии зацепления зубьев колес под углом 70° к линии их межосевого расстояния.
Для определения реакций в кинематических парах, разбиваем передаточный механизм на структурные группы. Отделяем от механизма два последних звена 4 и 5, а действие
отброшенных звеньев заменяем реакциями. На звено 5 со стороны стойки 0 действует реакция Р05, а на звено 4 – реакция со стороны кулисы. Для определения модуля неизвестных реакций строим многоугольник сил

Учитывая, что масштаб построения 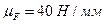 неизвестные реакции оказались равны Р05=83 Н, Р34=5095 Н. |P45|=|P34|.
неизвестные реакции оказались равны Р05=83 Н, Р34=5095 Н. |P45|=|P34|.
Далее определяем структурную группу состоящую из звеньев 3 и 2, дополнительно нагружаем силой Р43=-Р34, реакциями Р03 и Р12 которые раскладываем на нормальные и тангенциальные составляющие затем составляем уравнение равновесия для каждого из звеньев в форме моментов относительно центра шарнира В. Из этих уравнений:


Далее строим план сил:
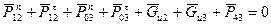
из плана находим
Р12=5288,48 Н
Р03=8485,68 Н
Р32=5280 Н
Далее рассматриваем Кривошип AB вместе с зубчатым колесом Z5 и соединяющих их с валом (n=1, p1=1, p2=1 по формуле Чебышева получаем W=0). Прикладываем к данной группе необходимые (известные и неизвестные) усилия, составляем уравнение моментов относительно центра A вращения вала кривошипа:

Из построенного плана находим Р01=10975,42 Н






