Об’єднуючи матричні рівняння першого та другого законів Кірхгофа в загальну систему, отримаємо узагальнене рівняння стану електричного кола, вигляд якого не залежить від його конфігурації і числа елементів:
Ці рівняння можна об’єднати в одне, якщо матриці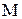 
і 
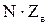розглядати як блоки однієї об’єднаної матриці параметрів схеми заміщення системи:
,
а матриці 
і 
розглядати як блоки однієї об’єднаної матриці вихідних параметрів режиму:
.
При цьому узагальнене рівняння стану прийме вигляд:
.
Тут матриця 
є квадратною і в звичайних умовах неособливою, тому отримане рівняння стану можна розв’язати відносно матриці струмів віток.
|
|
|
|
|
|
|
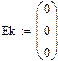
Загальне рівняння стану буде мати вигляд:
|
Система, що складається із (n-1) рівнянь, що зв’язують напруги вузлів відносно балансувального із задаючим струмом в вузлах і ЕРС у вітках, називається системою вузлових рівнянь. Вона широко використовується у практиці розрахунків усталених режимів складних електричних систем. Система вузлових рівнянь може бути отримана таким чином:
підставляючи у рівняння
,
що пов’язує матриці 
і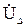 
, вираз із (1.1), отримаємо
;
розв’язавши отримане рівняння відносно струму 
(що можливо, оскільки ZB – квадратна і неособлива матриця), будемо мати
підставляючи вираз для 
в рівняння першого закону Кірхгофа, отримаємо
звідки
Визначимо матрицю провідності віток як
Позначимо
.
Отримана квадратна матриця порядку (n-1) називається матрицею вузлових провідностей. Вона дає можливість отримати кінцеву форму запису системи вузлових рівнянь (матричне вузлове рівняння):
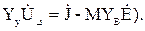
Розв’язавши дане рівняння відносно 
, можна розрахувати спад напруги на вітках схеми і знайти струми у вітках схеми.
Матриця вузлових провідностей з врахуванням b:
|
|
|
|
|
|
|
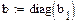
Система вузлових рівнянь:
|
Знайдемо напругу у вітках за системою вузлових рівнянь:
|
Розглянуті вузлові рівняння базувалися на рівняннях першого закону Кірхгофа і закону Ома для електричного кола. Їхнє використання для розрахунку усталеного режиму електричної системи дозволяє скоротити порядок розв’язуваної системи до (n-1) у порівнянні з використанням системи узагальнених рівнянь стану, що має порядок n. Ще однією можливістю зниження порядку розв’язуваної системи рівнянь є метод контурних рівнянь, основаних на другому законі Кірхгофа і законі Ома. Можливість застосування таких рівнянь, кількість яких дорівнює кількості незалежних контурів (k=m-n+1), обумовлена тим, що за відомими струмами у хордах графа схеми заміщення, кількість яких дорівнює кількості контурів, можна однозначно визначити струми у вітках дерева графа.
Виділивши блоки, що відповідають віткам дерева і хордам, можна записати рівняння першого закону Кірхгофа у вигляді:
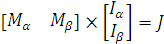
де, Іа, Іb – стовпці струмів у вітках дерева графа і хордах відповідно.
Звідси випливає, що:
 |
А оскільки:
 |
То ми отримаємо новий запис рівняння:
 |
При розбивці стовпця І на блоки держимо:
 |
Оскільки при виборі системи базисних контурів Nb=1, то
 | |||
 |
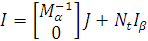і
Для визначення струму Іb як функції параметрів схеми заміщення, ЕРС у вітках і задавальних струмів у вузлах скористаємось матричним виразом другого закону Кірхгофа:
Підставимо в цей вираз матрицю струмів у вітках:
 |
Таким чином, отримуємо систему k взаємонезалежних рівнянь для визначення струмів у хордах:
 |
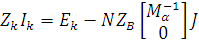Як відомо, для системи базисних контурів струми в хордах називають контурними. Позначивши Іk=Ib, остаточно запишемо математичний вираз системи контурних рівнянь:
де
 |
Квадратна неособлива матриця Zk порядку k називається матрицею контурних опорів.
Розв’язавши рівняння відносно Іk=Ib, можна визначити струми у вітках дерева схеми Ia, спади напруг на втках системи і напруги вузлів відносно балансувального вузла. В результаті вирішується задача визначення параметрів усталеного режиму електричної схеми.
Складемо контурне рівняння для заданої схеми:
|
|
|
|
|
Система контурних рівнянь:
