Складемо першу та другу матриці інценденції. Перша матриця інциденцій (по вузлам) М служить для узагальненого аналітичного представлення схеми з’єднань вузлів і віток (вершин і ребер) в анправленому графі (схемі електричної мережі).
В матриці з’єднань стрічки відповідають номерам вузлів, а стовпці – номерам віток. На перетині i -тої стрічки і j -того стовпця розміщуються коефіцієнти інцидентності (+1, якщо вузол і є початковою вершиною деякої вітки j; –1, якщо вузол і є кінцевою вершиною деякої вітки j; 0, якщо вузол і не є вершиною вітки j). Таким чином матриця дає повне уявлення про всі з’єднання віток в вузлах схеми.
Друга матриця інциденцій служить для узагальненого аналітичного представлення з’єднань віток схеми в незалежні замкнуті контури.
Стрічки другої матриці інциденцій N відповідають номерам незалежних замкнутих контурів схеми, а стовпці – номерам віток. Наявність з’єднань тут також визначається коефіцієнтами інцидентності +1, -1, 0. При цьому має бути вибраний напрям обходу кожного контуру. +1 показує, що дана вітка входить в склад даного контуру і має такий же напрям, що й обхід контуру. –1 показує, що дана вітка входить в склад даного контуру але має напрям, протилежний обходу контуру. 0 показує, що дана вітка не входить в склад даного контуру.
|
|
|
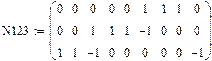
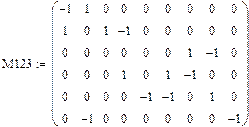
Перемноживши матрицю N на транспоновану матрицю М отримують нульову матрицю(матрицю, в якої всі елементи нулі) – це дає змогу робити перевірку правильності складання матриць інциденцій.
Матриці інциденцій для варіанту 1 з врахуванням балансуючого вузла 7:
|
|
|
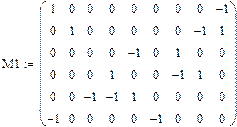
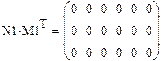
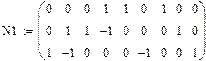
Матриці інциденцій для варіанту 2 з врахуванням балансуючого вузла 7:
|
|
|
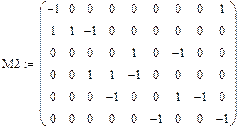
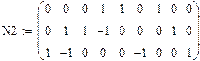
Надалі буде використовуватись тільки 2 варіант.
Перевіримо можливість визначення матриці N через матрицю М.
|
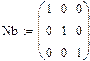
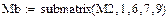
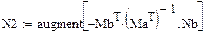
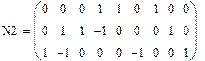
Стан лінійного електричного кола описується рівняннями законів Ома та Кірхгофа. Як відомо, закон Ома визначає взаємозв’язок параметрів кожної з віток кола. Для вітки, яка характеризується опором, ЕРС і протікаючим струмом, падіння наруги на вітці визначиться в відповідності з рівнянням:
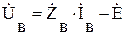(1.1)
Перший закон Кірхгофа визначає баланс струмів в кожному вузлі електричного кола і формулюється слідуючим чином: алгебраїчна сума струмів у вузлі дорівнює нулю. Для довільного вузла з джерелом струму J, в який входить k віток, рівняння першого закону Кірхгофа має вигляд:
Матриця інциденцій дозволяє записати перший закон Кірхгофа в матричній формі для схеми в цілому:
,
де І - струми в вітках, J – задаючі струми.
Другий закон Кірхгофа визначає баланс напруг в контурах електричного кола і формулюється слідуючим чином: алгебраїчна сума падінь напруг на вітках рівна нулю. Для довільного контуру, який містить l віток, рівняння другого закону Кірхгофа запишеться у вигляді:
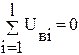
Система взаємно незалежних рівнянь другого закону Кірхгофа може бути записана у матричному вигляді:
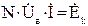
де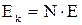 
– стовпець контурних ЕРС, які представляють собою алгебраїчні суми ЕРС віток, які входять в кожен незалежний контур.
Стан електричної системи повністю описується рівняннями законів Ома та Кірхгофа.
|
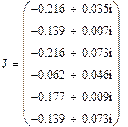
Знайдемо матрицю задаючих струмів:
|
|
|
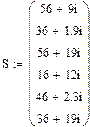
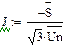
Перший закон Кірхгофа в матричній формі:
|
Другий закон Кірхгофа в матричній формі:
Приймаємо, що ЕРС в контурах схеми відсутня:
|
|
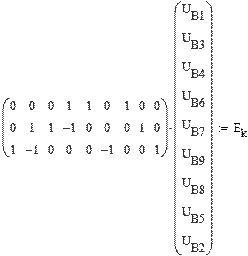
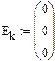
