Сведения, необходимые для выполнения работы. Подавляющее большинство измерений являются однократными

 

Подавляющее большинство измерений являются однократными. Системати­ческие погрешности могут существенно исказить результаты таких измерений. Поэтому обнаружению и устранению источников систематических погрешностей придается большое значение.

На практике очень часто приходится сталкиваться с необходимостью учета систематической погрешности, возникающей из-за несовершенства принятого метода измерений, эта погрешность известна как методическая. Для учета влия­ния методических погрешностей на результаты измерений обычно применяются математические зависимости, используемые для описания явления, положенного в основу измерения. В такой ситуации оценки погрешностей формул и физиче­ских констант, как правило, известны.

Систематические погрешности являются величинами детерминированными, поэтому в принципе всегда могут быть вычислены и учтены. Для исправления ре­зультатов измерений, содержащих систематическую погрешность, эти результа­ты складывают с поправками, равными систематическим погрешностям по вели­чине, но противоположными им по знаку. Поправки могут быть определены как экспериментально, так и теоретически. Поправки, определяемые эксперимен­тально, задаются в виде таблиц или графиков, теоретически - в виде формул. Ре­зультат измерений, полученный после внесения поправки, называется исправ­ленным результатом измерений.

В процессе выполнения настоящей работы измеряется ЭДС источника посто­янного напряжения, обладающего переменным внутренним сопротивлением. Значение измеряемой ЭДС лежит в диапазоне от 10 до 30 В. Для таких измерений можно использовать электромеханические и электронные аналоговые вольтмет­ры, цифровые вольтметры и компенсаторы (потенциометры) постоянного тока.

Электромеханические вольтметры и простые цифровые вольтметры выбира­ются для работы, если требования к точности измерений сравнительно невысоки, а значение измеряемого напряжения лежит в диапазоне от десятков милливольт до сотен вольт. Измерения в этом случае выполняются методом непосредствен­ной оценки. На практике очень удобно использовать простые и дешевые аналого­вые вольтметры, например магнитоэлектрической системы. В отличие от элект­ронных вольтметров, они не требуют дополнительного источника питания и более просты в эксплуатации, а по сравнению с электромеханическими вольтмет­рами других систем имеют лучшие характеристики.

Магнитоэлектрические вольтметры имеют линейную шкалу, характеризуют­ся весьма высокой точностью и чувствительностью, малым собственным потреб­лением энергии. На показания магнитоэлектрических вольтметров мало влияют колебания температуры окружающей среды и изменения напряженности внеш­него электромагнитного поля. Входное сопротивление магнитоэлектрических вольтметров постоянного тока относительно невелико и колеблется в диапазоне от 10 до 100 кОм, по этому показателю они уступают как электронным аналого­вым, так и цифровым вольтметрам.

Упрощенная электрическая схема магнитоэлектрического вольтметра приве­дена на рис. 1.2.1.

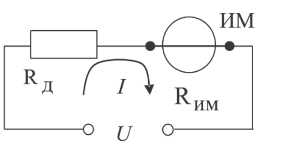
Рис. 1.2.1. Упрощенная схема магнитоэлектрического вольтметра

 

В состав схемы входят измерительный механизм (ИМ), облада­ющий собственным омическим сопротивлением R_ИМ, и добавочное сопротивле­ние R_д. Показания вольтметра отсчитываются по отклонению стрелки ИМ относительно неподвижной шкалы. Угол этого отклонения α определяется в со­ответствии с уравнением шкалы механизма и равен: α = 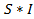, где S - чувствитель­ность ИМ, а I - значение тока, протекающего через него. Соответственно, для вольтметра получаем: α = .

Отметим, что ток, протекающий через ИМ, не должен превышать некоторой номинальной величины, которая называется током полного отклонения. Значе­ние этого тока для магнитоэлектрических ИМ лежит обычно в диапазоне от 1 мкА до 1 мА.

Как видно из соотношения (1.2.1), при использовании магнитоэлектрического вольтметра погрешность измерений в нормальных условиях определяется глав­ным образом инструментальной погрешностью вольтметра и методической погрешностью измерений. Инструментальная погрешность определяется клас­сом точности средства измерений, лежащим для магнитоэлектрических вольт­метров, как правило, в пределах от 0,2 до 2,5, а методическая погрешность - соотношением между входным сопротивлением вольтметра и внутренним со­противлением источника измеряемой ЭДС. Как указывалось, входное сопро­тивление магнитоэлектрического вольтметра сравнительно невелико, поэтому методическая составляющая погрешности может вносить определяющий вклад в результирующую погрешность измерений.

Для определения методической составляющей погрешности представим ис­точник измеряемого напряжения в виде активного двухполюсника (рис. 1.2.2), к которому подключен вольтметр, имеющий входное сопротивление R_BX = R_ИМ + Rд. Пусть активный двухполюсник имеет ЭДС - U₀ и внутреннее сопротивление - R_BH, тогда напряжение U_X на зажимах вольтметра можно вычислить по формуле:

 

Отсюда находим, что значение абсолютной методической погрешности ΔU равно:

 

ΔU = U_x-U₀ = 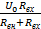- U₀ = -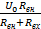

 

Кроме того, для модуля значения относительной методической погрешности δU имеем:

 

δU =

 

Как правило, R_BH<<R_BX, поэтому можно принять, что модуль относительной методической погрешности приблизительно равен:

 

δU =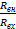

 

В рассматриваемом случае методическая погрешность проявляется как систе­матическая, поэтому она может быть исключена внесением поправки П = -ΔU, прибавленной к показанию вольтметра.

Даже после внесения поправки всегда остается неисключенный остаток мето­дической погрешности, в нашем случае такой остаток может возникнуть из-за от­личия истинных значений сопротивлений от тех, которые использованы при рас­четах. Кроме того, в качестве составляющих неисключенной систематической погрешности могут выступать систематические погрешности средства измерений и систематические погрешности, вызванные другими источниками. При опреде­лении границ неисключенной систематической погрешности результата измере­ний все такие составляющие рассматриваются как случайные величины и строит­ся их композиция. Мы не будем здесь рассматривать правила построения такой композиции и остановимся только на важном частном случае.

Пусть значение допускаемого предела основной абсолютной инструменталь­ной погрешности, определяемой классом точности средства измерений, равно Δ_пр, а значение неисключенного остатка абсолютной методической составляющей по­грешности равно Δ_м, тогда границы абсолютной погрешности результата измере­ний Δ_изм можно с приемлемой точностью вычислить по формуле

 

Δ_изм =