;
;
;
Т2 = 0,12 Т3 = 0,012
Амплитуда частотной передаточной функции находится как отношение модулей числителя и знаменателя, а фаза – как разность аргументов числителя и знаменателя.
| Передаточная функция | Амплитуда | Фаза |
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
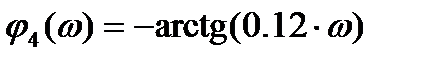
Задавая значения частот 
, вычисляются значения 
и 
. В полярной системе координат строится АФЧХ (рис. 10).
Составим таблицу значений:
| ω | A 1 (ω) | A 2 (ω) | A 3 (ω) | A 4 (ω) | A 5 (ω) | φ 1 (ω) | φ 2 (ω) | φ 3 (ω) | φ 4 (ω) | φ 5 (ω) | A(ω) | φ(ω) |
| 19.05 | 19.05 | |||||||||||
| 0.1 | 18.52 | 0.23 | -1.5 | -0.7 | -7.6 | -15 | 1.852 | -24.5 | ||||
| 1.1 | 0.05 | 0.97 | 17.17 | 0.44 | -1.5 | -1.5 | -15 | -28.5 | 0.92 | -46.1 | ||
| 1.23 | 0.035 | 0.94 | 15.46 | 0.62 | -1.54 | -2.3 | -22 | -39.7 | 0.62 | -65.2 | ||
| 1.38 | 0.026 | 0.9 | 13.74 | 0.76 | -1.55 | -3 | -28.5 | -48.7 | 0.44 | -81 | ||
| 1.55 | 0.02 | 0.86 | 12.2 | 0.87 | -1.55 | -3.8 | -34.4 | -55.8 | 0.32 | -94.8 | ||
| 1.74 | 0.017 | 0.81 | 10.87 | 0.96 | -1.55 | -4.6 | -39.7 | -61.6 | 0.26 | -106.5 | ||
| 1.94 | 0.015 | 0.77 | 9.74 | -1.56 | -5.3 | -44.5 | -65.8 | 0.22 | -116.2 | |||
| 2.15 | 0.013 | 0.72 | 8.8 | 1.1 | -1.56 | -6 | -48.7 | -69.4 | 0.18 | -124.6 | ||
| 2.36 | 0.012 | 0.68 | 1.13 | -1.57 | -6.8 | -52.4 | -72.4 | 0.15 | -132.1 | |||
| 2.58 | 0.01 | 0.64 | 7.33 | 1.17 | -1.57 | -7.6 | -55.8 | -74.9 | 0.12 | -138.8 | ||
| 3.7 | 0.007 | 0.98 | 0.49 | 1.3 | -1.57 | -11.3 | -67.7 | -82.7 | 0.086 | -161.8 | ||
| 4.86 | 0.005 | 0.97 | 0.35 | 3.88 | 1.36 | -1.57 | -15 | -74.9 | -86.9 | 0.044 | -177.3 | |
| 0.004 | 0.96 | 0.31 | 3.13 | 1.4 | -1.57 | -18.5 | -79.5 | -89.5 | 0.022 | -187.8 |
Вывод: система устойчивая, так как АФЧХ разомкнутой системы не охватывает точку с координатами (-1;0)
Рис.10. График АФЧХ
Исследование САР по логарифмическому критерию
Найдем параметры ЛАХ:
| Передаточная функция | lg (ωСР) | 20lg k |
|
| 0.62 | - |
| -0.98 | |
|
| 1.92 | |
|
| 0.92 | |
| 0.62 | 25.6 |
Построим ЛАХ и ЛФХ отдельных звеньев и результирующие ЛАХ и ЛФХ (рис. 11)
Вывод: система устойчива, т.к. ЛАХ разомкнутой системы пересекает ось абсцисс раньше, чем ЛФХ, спадая окончательно, переходит через значение -π.
Рис.11. График ЛАХ и ЛФХ
Раздел 5. Исследование САР в среде Simulink
Построение графика переходного процесса
(Без корректирующего звена)
Проведём обратное преобразование Лапласса:
Полученное дифференциальное уравнение решаем с помощь MathLab Simulink
График переходного процесса
Построение графика переходного процесса
(с корректирующим звеном)
Составим уравнение замкнутой системы:
Проведём обратное преобразование Лапласса:
Полученное дифференциальное уравнение решаем с помощь MathLab Simulink
График переходного процесса
Проверка расчетов с помощью моделирования системы в среде MATLABSimulink
Структурная схема САР в среде Simulink(Без корректирующего звена)
График переходного процесса системы
ЛАХ и ЛФХ
АФЧХ
Структурная схема САР в среде Simulink
(с корректирующим звеном)
График переходного процесса системы
ЛАХ и ЛФХ
АФЧХ
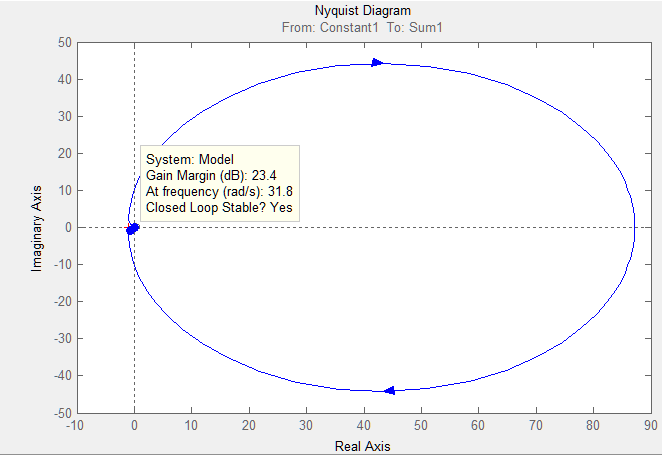
Вывод: введение корректирующего звена увеличило запасы устойчивости по амплитуде и по фазе, а также уменьшило величину перерегулирования. С введением корректирующего звена САУ стала более устойчивой.
Заключение
В данной работе описана работа системы автоматического регулирования угловой скорости двигателя постоянного тока независимого возбуждения, выведены передаточные функции для данной системы. Выполнена проверка системы на устойчивость по частотным критериям Михайлова, Найквиста, логарифмическому критерию и алгебраическому критерию Гурвица. Введение в САУ корректирующего звена, увеличило запасы устойчивости по амплитуде и по фазе. С помощью Simulinkбыла проверена система на устойчивость и на качество переходного процесса, как и для исходной системы автоматического управления, так и для скорректированной системы автоматического управления.
Список используемой литературы:
1. Щербаков В.С. Конспект лекций по ТАУ
2. Щербаков В.С., Сухарев Р.Ю. «Методические указания по выполнению курсовых работ» - 2011г.
3. Александров Ю.В. «Основы автоматики и автоматизация производственных процессов в дорожном строительстве». - 1974 г.
4. Герман-Галкин С.Г. «Компьютерное моделирование полупроводниковых систем MatLab6.0»
