Т2 = 0,12 Т3 = 0,012
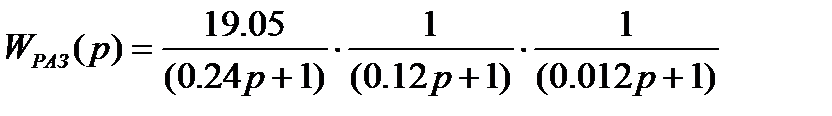
Амплитуда частотной передаточной функции находится как отношение модулей числителя и знаменателя, а фаза – как разность аргументов числителя и знаменателя.
| Передаточная функция | Амплитуда | Фаза |
| 
| 
|
| 
| 
|
| 
| 
|
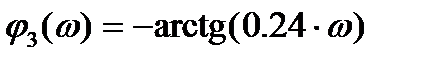
Задавая значения частот 
, вычисляются значения 
и 
. В полярной системе координат строится АФЧХ (рис. 5).
Составим таблицу значений:
| ω | A 1 (ω) | A 2 (ω) | A 3 (ω) | φ 1 (ω) | φ 2 (ω) | φ 3 (ω) | A(ω) | φ(ω) |
| 19.05 | 19.05 | |||||||
| 18.52 | -0.7 | -7.6 | -15 | 18.52 | -23.3 | |||
| 0.97 | 17.17 | -1.5 | -15 | -28.5 | 16.65 | -45 | ||
| 0.94 | 15.46 | -2.3 | -22 | -39.7 | 14.53 | -64 | ||
| 0.9 | 13.74 | -3 | -28.5 | -48.7 | 12.37 | -80.2 | ||
| 0.86 | 12.2 | -3.8 | -34.4 | -55.8 | 10.5 | -94 | ||
| 0.81 | 10.87 | -4.6 | -39.7 | -61.6 | 8.8 | -105.9 | ||
| 0.77 | 9.74 | -5.3 | -44.5 | -65.8 | 7.5 | -115.6 | ||
| 0.72 | 8.8 | -6 | -48.7 | -69.4 | 6.34 | -124.1 | ||
| 0.68 | -6.8 | -52.4 | -72.4 | 5.44 | -131.6 | |||
| 0.64 | 7.33 | -7.6 | -55.8 | -74.9 | 4.7 | -138.3 | ||
| 0.98 | 0.49 | -11.3 | -67.7 | -82.7 | 2.4 | -161.7 | ||
| 0.97 | 0.35 | 3.88 | -15 | -74.9 | -86.9 | 1.32 | -176.8 | |
| 0.96 | 0.31 | 3.13 | -18.5 | -79.5 | -89.5 | 0.93 | -187.5 |
Вывод: система не устойчивая, так как АФЧХ разомкнутой системы охватывает точку с координатами (-1;0)
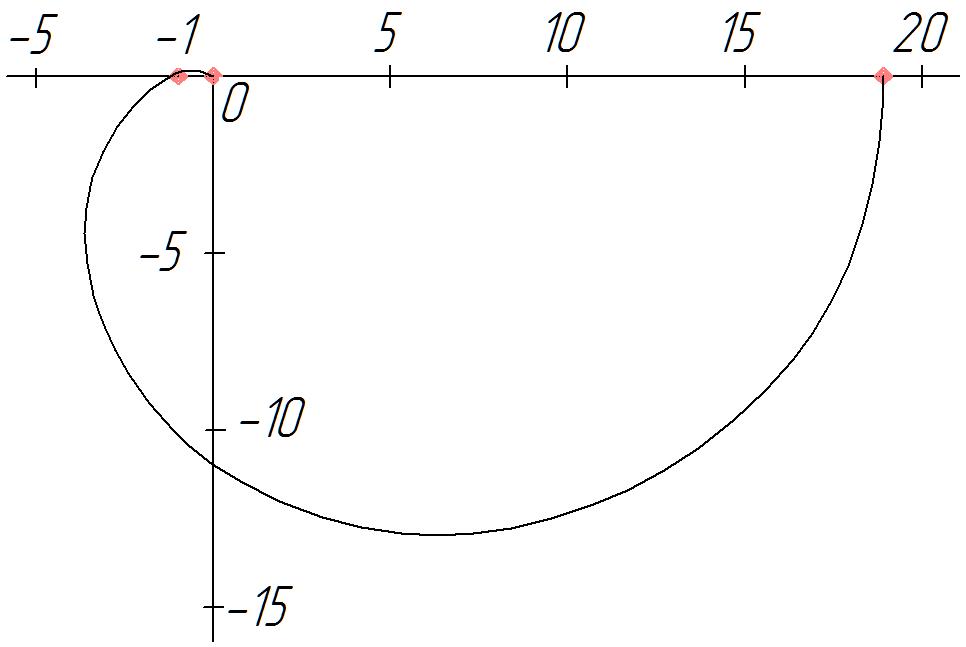
Рис.5. График АФЧХ
Исследование САР по логарифмическому критерию
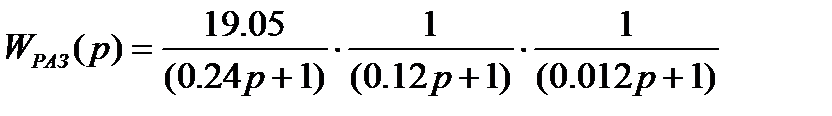
Найдем параметры ЛАХ:
| Передаточная функция | lg (ωСР) | 20lg k |
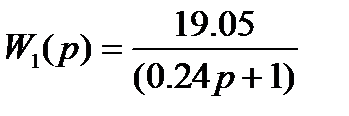
| 0.62 | 25,6 |
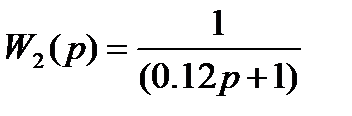
| 0.92 | |
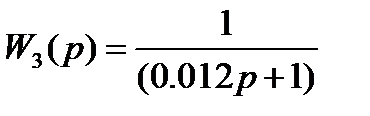
| 1.92 |
Построим ЛАХ и ЛФХ отдельных звеньев и результирующие ЛАХ и ЛФХ (рис. 6)
Вывод: система устойчива, т.к. ЛАХ разомкнутой системы пересекает ось абсцисс раньше, чем ЛФХ, спадая окончательно, переходит через значение -π.
Рис.6. График ЛАХ и ЛФХ
Корректирующее звено 
R4
R2
R1
Рис.7 Активное корректирующее звено
Дано: С = 9,35·10–6 Ф; R4 = 2,55·104 Ом; R2 = 106 Ом.
Передаточная функция активного корректирующего звена:
WКЗ(p) = k0 
k0 = 
= 
= 
= 2.06
T01 = R4 
C = 2.55 
104 9.35 10-6 = 0.238
T02 = (R4 + R2) C = (2.55 104 + 100 
104) 9.35 10-6 = 9.588
WКЗ(p) = 2.06 
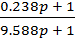
Передаточная функция разомкнутой системы с корректирующим звеном:
где 
Раздел 4. Исследование САР с корректирующим звеном
Составим структурно-математическую схему системы стабилизации с
корректирующим звеном, заменив элементы схемы на их передаточные функции (рис.8)
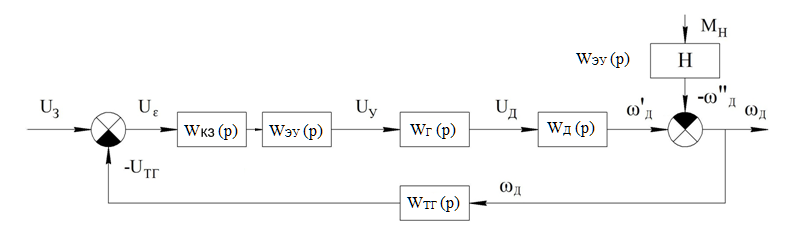
Рис.8. Структурно-математическая схема системы стабилизации с КЗ
Исследование САР по критерию Гурвица
Для исследования устойчивости замкнутой САР по критерию устойчивости Гурвица необходимо составить определитель Гурвица. Для этого понадобится характеристическое уравнение замкнутой системы.
Составим передаточную функцию разомкнутой системы, для чего перемножим все передаточные функции, включая обратную связь.
После подстановки численных значений получим:
Wраз (p) = 2.06 
10 
0.45
Wраз (p) = 2.06 
Wраз (p) = 2.06 
Wраз (p) = 
Составим характеристическое уравнение:
= 0
где: a0 = 0.0034, a1 = 0.32, a2 = 3.55, a3 = 19.27, a4 = 40.24
Определитель Гурвица:
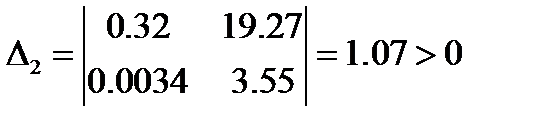
Вывод: система устойчива, так как не имеет отрицательных миноров.
Исследование САР по критерию Михайлова
Wраз (p) =
= 0
Производим замену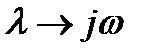 
= 0
UD(𝜔) = 
j VD(𝜔) = 
Составим таблицу:
| ω | UD (ω) | i×VD (ω) | ω | UD (ω) | i×VD (ω) |
| 40.24 | -586 | -790 | |||
| 36.7 | 18.9 | -835 | -2175 | ||
| -850 | -4518 | ||||
| 8.6 | -400 | -8062 | |||
| -15.7 | 56.6 | -793 | -13050 | ||
| -46.4 | 56.3 | -19710 | |||
| -83 | 46.5 | -28290 | |||
| -125 | -39040 | ||||
| -173 | -9.7 | -52180 | |||
| -225 | -60 | -67960 | |||
| -281 | -127 | -86630 |
Вывод: Система устойчива. Годограф огибает против часовой стрелки начало координат и проходит через 4 квадранта, порядок характеристического уравнения = 4.
Рис.9. График годографа Михайлова
