
В формуле (2):
Левая часть – площадь криволинейной трапеции aABb
Правая часть – площадь прямоугольника с основанием b-a и высотой f(c)
Таким образом, формула (2) геометрически означает, что можно всегда подобрать на дуге AB такую точку С с абсциссой с, заключенной между a и b, что площадь соответствующего прямоугольника aDEb с высотой сС будет в точности равна площади криволинейной трапеции aABb.
Число  - называется средним значением функции f(x) на отрезке [a,b].
- называется средним значением функции f(x) на отрезке [a,b].
Из (2) имеем  (3)
(3)
Следствие
Пусть  и
и  . Так как
. Так как  , при a<b из (2) имеем
, при a<b из (2) имеем  (4)
(4)
Интегрирование по частям в определенном интеграле
Пусть u(x) и v(x) непрерывные дифференцируемые функции на отрезке [a,b]. Имеем d[u(x)v(x)]=v(x)du(x)+u(x)dv(x). Интегрируя, это равенство в пределах от a до b и учитывая, что du(x)=u’(x)dx и dv(x)=v’(x)dx находим

Отсюда получаем формулу интегрирования по частям в определенном интеграле
 (1)
(1)
Для краткости употребляется выражение 
Пример

Замена переменной в определенном интеграле
Пусть дан определенный интеграл
 (1), где f(x) непрерывна на отрезке [a,b].
(1), где f(x) непрерывна на отрезке [a,b].
Ввели новую переменную t, связанную с х соотношением  (2)
(2)
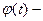 непрерывная дифференцируемая функция на отрезке
непрерывная дифференцируемая функция на отрезке 
Если при этом
1) При изменении t от  до
до  переменная х меняется от a до b, то есть
переменная х меняется от a до b, то есть  (3)
(3)
2) Сложная функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке 
Тогда справедлива формула  (4)
(4)
Доказательство
Рассмотрим сложную функцию  , где F(x) – первообразная для f(x), то есть F’(x)=f(x)
, где F(x) – первообразная для f(x), то есть F’(x)=f(x)
Применяя правило дифференцирования сложной функции, получим

Следовательно функция  - первообразная для функции
- первообразная для функции  .
.
Отсюда, на основании формулы Ньютона-Лейбница, учитывая равенство (3), получаем

Замечание
При вычислении определенного интеграла с помощью замены переменной нет необходимости возвращаться к прежней переменной, достаточно ввести новые пределы интегрирования по формулам (3).
Пример


Приложения определенного интеграла
Определенный интеграл можно применять в следующих задачах:
- вычисление площадей, ограниченных некоторыми линиями;
- вычисление длин дуг линий;
- вычисление объемов тел по известным площадям поперечных сечений;
- вычисление объемов тел вращения;
- вычисление поверхностей тел вращения;
- вычисление координат центра тяжести плоской фигуры;
- вычисление моментов инерции линии, круга, цилиндра и т.д.
Площадь в прямоугольных координатах
Задача 1 Найти площадь S криволинейной трапеции aABb, ограниченной данной непрерывной линией y=f(x), отрезком [a,b] ооси ОХ и двумя вертикалями x= a и x=b, если 

Решение
На основании геометрического смысла определенного интеграла имеем
 (1), где y=f(x) – данная функция
(1), где y=f(x) – данная функция
Рассмотрим другой способ обоснования формулы (1).
Будем рассматривать площадь S как переменную величину, образованную перемещением текщей ординаты xM=y из начального положения aA в конечное положение bB. Давая текущей абсциссе x приращение  , получим приращение площади
, получим приращение площади  , представляющее собой площадь вертикальной полосы xMM’x’, заключенной между ординатами в точках x и
, представляющее собой площадь вертикальной полосы xMM’x’, заключенной между ординатами в точках x и  .
.
Дифференциал площади dS есть главная линейная часть приращения  при
при  и очевидно равен площади прямоугольника с основанием dx и высотой y. Поэтому
и очевидно равен площади прямоугольника с основанием dx и высотой y. Поэтому
dS=ydx (2)
Интегрируя равенство (2) в пределах от x=a до x=b получаем формулу (1) 
В этом случае показано применение метода дифференциала, сущность которого заключается в том, что сначала из элементарных соображений составляется дифференциал искомой величины, а затем после интегрирования в соответствующих пределах находится значение самой искомой величины.
Задача 2
Найти площадь обрасти, ограниченной двумя непрерывными линиями  и двумя вертикалями x=a и x=b.
и двумя вертикалями x=a и x=b.

Решение.
Будем предполагать, что  - неотрицательные функции на отрезке [a,b].
- неотрицательные функции на отрезке [a,b].
Искомую площадь S можно рассматривать, как разность площадей двух криволинейных трапеций, ограниченных данными линиями. Поэтому
 (3)
(3)
Примеры
- Вычислить площадь, ограниченную линиями
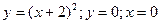
|
Решение
Отрезок интегрирования [-2,0], тогда 
- Вычислить площадь, ограниченную линиями


Решение
Отрезок интегрирования [0,2], тогда 
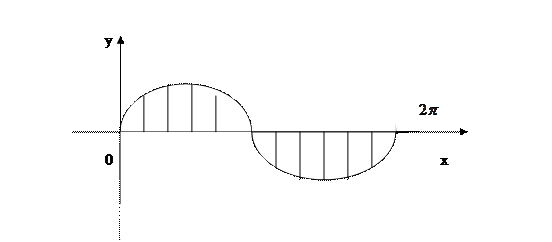
3. Вычислить площадь, ограниченную графиком функции y=sinx на отрезке  и ОХ.
и ОХ.
Решение
Отрезок интегрирования  разбиваем на два отрезка и
разбиваем на два отрезка и  , где
, где 

 =2+2+4
=2+2+4
4. Вычислить площадь, ограниченную параболой  и прямой x+y=3.
и прямой x+y=3.
|

Решение
Отрезок интегрирования  , так как точки пересечения линий
, так как точки пересечения линий  , определяются при решении системы уравнений
, определяются при решении системы уравнений  . На основании формулы (3) находим
. На основании формулы (3) находим

5. Найти площадь области, ограниченной эллипсом  . В виду симметрии можно ограничиться вычислением ¼ площади.
. В виду симметрии можно ограничиться вычислением ¼ площади.

Решение
Отрезок интегрирования  ,
,

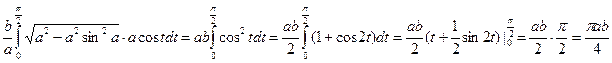
Тогда 
6. Найти площадь, ограниченную первой аркой циклоиды 

Решение
Отрезок интегрирования  ,
,


 .
.






