Лекция 9. Определенный интеграл. Общее определение. Основные свойства. Основные методы вычисления определенных интегралов.
К понятию определенного интеграла приводят такие задачи, как:
- задача о площади криволинейной трапеции;
- задача о вычислении длины прямолинейного пути по заданной скорости;
- задача о вычислении объемов;
- задача о вычислении массы прямолинейного стержня и т.д.
Рассмотрим задачу о вычислении площади криволинейной трапеции
Рассмотрим криволинейную трапецию aABb, то есть плоская фигура, ограниченная графиком функции y=f(x), отрезками аА, вВ, прямыми x=a, x=b и осью ОХ.
Разобьем отрезок [a,b] точками 
на n произвольных отрезков, то есть 
. Длину каждого отрезка обозначим через 
. На каждом отрезке 
построим прямоугольник высотой 
, где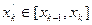 
, - значение функции в этой точке.
- площадь такого прямоугольника. Составим сумму таких произведений
(1) – интегральная сумма для функции f(x) на отрезке [a,b]
Интегральная сумма (1) выражает площадь ступенчатой фигуры и приближенно заменяет площадь криволинейной трапеции aABb.
Функция y=f(x) – непрерывная и площадь построенной фигуры при достаточно малых ”почти совпадает” с площадью рассматриваемой криволинейной трапеции. Можно для [a,b] выбирать различные и 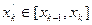и таким образом получать последовательность разбиений и последовательность интегральных сумм. Можно доказать, что существует предел S переменной , когда 
, а длина 
, то есть 
. Предел S – площадь криволинейной трапеции.
Определение
Предел S интегральной суммы для функции y=f(x) на отрезке [a,b], когда число n отрезков неограниченно возрастает, а наибольшая длина отрезка называют определенным интегралом от функции y=f(x) на отрезке [a,b].
Обозначение 
(2)
a – нижний предел интегрирования;
b – верхний предел интегрирования;
[a,b] – отрезок интегрирования;
f(x) – подынтегральная функция;
x – переменная интегрирования.
Функцию f(x) интегрируема на отрезке [a,b], если для нее существует предел (2).
Замечание
Если f(x) интегрируема на отрезке [a,b], то f(x) интегрируема и на 
.
Таким образом, возвращаясь к задаче о площади криволинейной трапеции, можно сказать, что она может быть вычислена с помощью определенного интеграла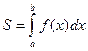 
.
Из определения следует, что величина определенного интеграла не зависит от обозначения переменной интегрирования
= 
=...= 
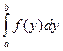и т.д.
Формула Ньютона-Лейбница
Вычисление определенного интеграла основано на применении формулы Ньютона-Лейбница.
Пусть f(x) – интегрируема на отрезке [a,b] и F(x) – одна из первообразных функции f(x), то есть f(x)=F’(x). Тогда приращение первообразной на отрезке [a,b], то есть F(b)-F(a) равно значению определенного интеграла
(1)
Другая форма записи 
- двойная подстановка от a до b
Таким образом, чтобы вычислить определенный интеграл, достаточно найти одну из первообразных подынтегральной функции и вычислить ее значение сначала при x=b, затем при x=a и из первого результата вычесть второй.
Пример
Если F(x)= 
, тогда 
Следовательно, от выбора первообразной значение интеграла не зависит.
Определенный интеграл с переменным верхним пределом
Пусть f(x0 непрерывна на отрезке [a,b]. Рассмотрим интеграл
(1), где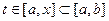 
(во избежании путаницы, переменная интегрирования обозначена другой буквой)
Если F(x) – первообразная функции f(x), то есть F’(x)=f(x), то согласно формуле Ньютона-Лейбница имеем
(2), отсюда
Следовательно
Производная определенного интеграла с переменным верхним пределом по этому пределу равна значению подынтегральной функции для этого предела:
(3)
Таким образом, интеграл
(4)
является первообразной для подынтегральной функции f(x).
Отметим, что из формулы (2) следует, что Ф(а)=0, то есть Ф(х) есть та первообразная для функции f(x), которая обращается в 0 при х=а.
Пример
Рассмотрим определенный интеграл с переменным нижним пределом
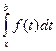, где 
На основании формулы Ньютона-Лейбница имеем
Таким образом, производная определенного интеграла с переменным нижним пределом по этому пределу равна значению подынтегральной функции для этого предела, взятому с обратным знаком.
