При выводе основных свойств определенного интеграла исходим из формулы Ньютона-Лейбница
(1), где f(x) – непрерывна на отрезке [a,b], f(x)=F’(x).
Разобьем свойства определенного интеграла на группы.
А. Общие свойства
I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, то есть
= 
=...= 
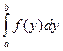II. Определенный интеграл с одинаковыми пределами интегрирования равен 0, то есть 
=F(a)-F(a)=0
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный. Действительно, переставляя пределы интегрирования, в силу формулы (1), получим
(2)
Б. Свойство аддитивности
IV. Если отрезок интегрирования [a,b] разбить на конечное число частичных отрезков, то определенный интеграл, взятый по отрезку [a,b] равен сумме определенных интегралов, взятых по всем частичным отрезкам.
Пусть 
, где 
Полагая F’(x)=f(x)
(3)
Замечание
Формула (3) справедлива, если с лежит вне отрезка [a,b] и f(x) непрерывна на отрезках [a,c],[c,b].
В. Свойства линейности
V. Постоянный множитель можно выносить за знак интеграла
Пусть F(x) – первообразная для f(x) на [a,b], где А – постоянная величина, тогда AF(x) – первообразная для Af(x), так как [AF(x)]’=AF’(x)=Af(x). Получаем
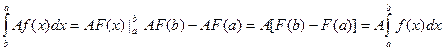
VI. Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
Рассмотрим алгебраическую сумму функций f(x)+g(x)-h(x) (4), где f(x),g(x),h(x) – непрерывные функции.
F(x), G(x), H(x) – их первообразные, то есть F’(x)=f(x), G’(x)=g(x), H’(h)=h(x), тогда F(x)+G(x)-H(x) – первообразная для f(x)+g(x)-h(x), так как
[F(x)+g(x)-H(x)]’=F’(x)+G’(x)-H’(x)=f(x)+g(x)-h(x)
Отсюда получаем
Г. Свойства монотонности
VII. Если подынтегральная функция определенного интеграла непрерывна и неотрицательна, а верхний предел интегрирования больше нижнего или равен ему, то определенный интеграл также неотрицателен.
Пусть 
при 
. Так как F’(x)=f(x)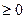 
, то F(x) – неубывающая функция. В таком случае при 
имеем 
VIII. Неравенство между непрерывными функциями можно интегрировать поэлементно при условии, что верхний предел интегрирования больше нижнего.
Пусть 
при , f(x),g(x) – непрерывные функции на отрезке [a,b].
Так как 
, то в силу свойств VI и VIII имеем
, отсюда 
Замечание
Пусть f(x) – знакопеременная непрерывная функция на отрезке [a,b], где b>a.
В силу свойства аддитивности IV и учитывая геометрический смысл интеграла имеем
- площади соответствующих криволинейных трапеций.
Таким образом, определенный интеграл, в общем случае при a<b представляет собой алгебраическую сумму площадей, соответствующих криволинейных трапеций, где площади трапеций, расположенных выше оси ОХ, берутся со знаком +, а площади трапеций, расположенных ниже оси ОХ, - со знаком -.
Теорема о среднем
Теорема
Определенный интеграл от непрерывной функции равен произведению длины отрезка интегрирования на значение подынтегральной функции при некотором промежуточном значении аргумента.
Доказательство:
В силу формулы Ньютона-Лейбница имеем
(1), где F’(x)=f(x)
Применяя к разности первообразных теорему о конечном приращении функции получим
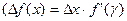, где 
F(b)-F(a)=(b-a)F’(c)=(b-a)f(c), где a<c<b, отсюда
(2), где a<c<b
