В приложениях математического анализа встречаются так называемые односторонние пределы.
Введем понятия левой и правой окрестностей точки а (а – число).
Определение 1
1) любой интервал  , правым концом которого является точка а, называется ее левой окрестностью.
, правым концом которого является точка а, называется ее левой окрестностью.
2) любой интервал  , левым концом которого является точка а, называется ее правой окрестностью.
, левым концом которого является точка а, называется ее правой окрестностью.
Запись  означает, что х принимает лишь значения, принадлежащие некоторой левой окрестности точки а, то есть
означает, что х принимает лишь значения, принадлежащие некоторой левой окрестности точки а, то есть 
Запись  означает, что х принимает лишь значения, принадлежащие некоторой правой окрестности точки а, то есть
означает, что х принимает лишь значения, принадлежащие некоторой правой окрестности точки а, то есть 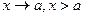
Определение 2
1) Формула 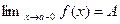 , где функция f(x) определена на множестве Х и а – предельная точка этого множества, а А – число, обозначает, что
, где функция f(x) определена на множестве Х и а – предельная точка этого множества, а А – число, обозначает, что 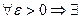
 , такая, что |f(x)-A|<
, такая, что |f(x)-A|<  при
при 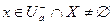 (1)
(1)
2) Формула  , где функция f(x) определена на множестве Х и а – предельная точка этого множества, а B – число, обозначает, что
, где функция f(x) определена на множестве Х и а – предельная точка этого множества, а B – число, обозначает, что 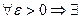
 , такая, что |f(x)-B|<
, такая, что |f(x)-B|<  при
при 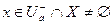 (2)
(2)
Для чисел A и B используется следующая символическая запись A=f(a-0), B=f(a+0)

Определение 3
Под окрестностью символа  понимается любой интервал
понимается любой интервал  , и под окрестностью символа
, и под окрестностью символа  понимается любой интервал
понимается любой интервал 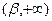 .
.
Формулы
 и
и  (3) интерпретируются таки образом
(3) интерпретируются таки образом
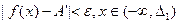 и
и 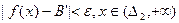 , где
, где  - произвольно,
- произвольно,  и
и 
Пример 
Имеем  и
и 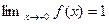

Замечание
Для существования предела функции f(x) при  (а – число) необходимо и достаточно выполнение равенства f(a-0)=f(a+0).
(а – число) необходимо и достаточно выполнение равенства f(a-0)=f(a+0).
Бесконечно малые функции
Определение
Функция  называется бесконечно малой при
называется бесконечно малой при  (а – вещественное число или символ
(а – вещественное число или символ  ), если
), если  , что
, что  .
.
Это эквивалентно  (2) или
(2) или  (3).
(3).
Аналогично определяется бесконечно малая функция при  ,
,  ,
, 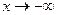 ,
, 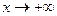 .
.
Замечание
Если 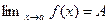 (4), то в силу определения предела функции получаем, что f(x)-A – бесконечно малая функция. Таким образом, из (4) получаем представление функции f(x), имеющей предел А при
(4), то в силу определения предела функции получаем, что f(x)-A – бесконечно малая функция. Таким образом, из (4) получаем представление функции f(x), имеющей предел А при  в виде
в виде
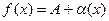 (5), где
(5), где  .
.
Обратно, если для функции f(x) справедлива формула (5), то число А является пределом функции при  . Из формулы (5) вытекает важная лемма о сохранении знака функции.
. Из формулы (5) вытекает важная лемма о сохранении знака функции.
Лемма
Если 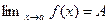 , то в некоторой окрестности
, то в некоторой окрестности  знак функции f(x) совпадает со знаком числа А.
знак функции f(x) совпадает со знаком числа А.
Действительно, пусть 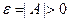 . Выбирая окрестность
. Выбирая окрестность  так, чтобы
так, чтобы 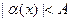 при
при  в силу равенства (5) будем иметь
в силу равенства (5) будем иметь
 , где
, где 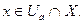
Sgn x=+1, при x>0
Sgn 0=0
Sgn x=-1, при x<0
Замечание Функция  в некоторой окрестности
в некоторой окрестности  по смыслу определения (1) является бесконечно малой при
по смыслу определения (1) является бесконечно малой при  .
.
Бесконечно большие функции
Определение
Функция f(x) называется бесконечно большой при  (а – число или символ
(а – число или символ 
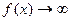 при
при  (1), если для
(1), если для  точки a, что |f(x)|>E при
точки a, что |f(x)|>E при 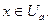 (2) для всех допустимых значений аргумента х.
(2) для всех допустимых значений аргумента х.
Если функция f(x) - бесконечно большая при  , то условно пишут
, то условно пишут
 (3)
(3)
Пример 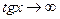 при
при 
Записи  и
и  соответственно означают
соответственно означают
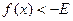 при
при 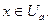 и
и  при
при 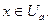
Лемма
- Если
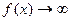 при
при  , то
, то 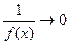 при
при 
- Если
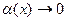 при
при  , то
, то  при
при 






