Лекция 3. Общие понятия и определения. Классификация функций. Предел функции. Бесконечно малые и бесконечно большие функции. Основные теоремы о бесконечно малых функциях.
Функция
При решении различных задач обычно приходится иметь дело с постоянными и переменными величинами.
Определение
Постоянной величиной называется величина, сохраняющая одно и тоже значение или вообще или в данном процессе: в последнем случае она называется параметром.
Переменной величиной называется величина, которая может принимать различные числовые значения.
Понятие функции
При изучении различных явлений обычно имеем дело с совокупностью переменных величин, которые связаны между собой так, что значения одних величин (независимые переменные) полностью определяют значения других (зависимые переменные и функции).
Определение
Переменная величина y называется функцией (однозначной) от переменной величины x, если они связаны между собой так, что каждому рассматриваемому значению x соответствует единственное вполне определенное значение величины y (сформулировал Н.И.Лобачевский).
Обозначение y=f(x) (1)
x – независимая переменная или аргумент;
y – зависимая переменная (функция);
f – характеристика функции.
Совокупность всех значений независимой переменной, для которых функция определена, называется областью определения или областью существования этой функции. Областью определения функции может быть: отрезок, полуинтервал, интервал, вся числовая ось.
Примеры:
- Формула площади круга
Каждому значению радиуса соответствует значение площади круга. Площадь – функция от радиуса, определенная в бесконечном интервале 
2. Функция 
(2). Функция определена при 
Для наглядного представления поведения функции строят график функции.
Определение
Графиком функции y=f(x) называется множество точек M(x,y) плоскости OXY, координаты которых связаны данной функциональной зависимостью. Или график функции – это линия, уравнением которой служит равенство, определяющее функцию.
Например, график функции (2) – полуокружность радиуса 2 с центром в начале координат.
Простейшие функциональные зависимости
Рассмотрим несколько простейших функциональных зависимостей
- Прямая функциональная зависимость
Определение
Две переменные величины называются прямо пропорциональными, если при изменении одной из них в некотором отношении, другая изменяется в том же соотношении.
y=kx, где k – коэффициент пропорциональности.
График функции
- Линейная зависимость
Определение
Две переменные величины связаны линейной зависимостью, если 
, где 
- некоторые постоянные величины.
График функции
- Обратная пропорциональная зависимость
Определение
Две переменные величины называются обратно пропорциональными, если при изменении одной из них в некотором отношении, другая изменяется в обратном отношении.
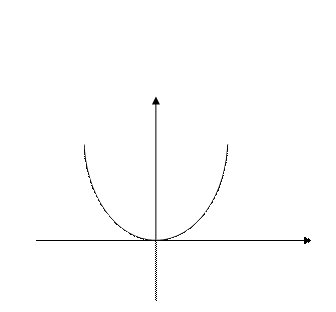
- Квадратичная зависимость
Квадратичная зависимость в простейшем случае имеет вид 
, где k – некоторая постоянная величина. График функции – парабола.
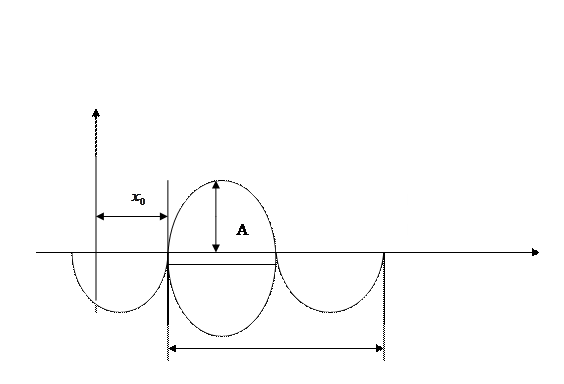
- Синусоидальная зависимость.
При изучении периодических явлений важную роль играет синусоидальная зависимость
- функция называется гармоникой.
A – амплитуда;
- частота;
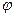- начальная фаза.
Функция периодическая с периодом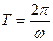 
. Значения функции в точках x и x+T, отличающихся на период, одинаковы.
Функцию можно привести к виду 
, где 
. Отсюда получаем, что графиком гармоники является деформированная синусоида с амплитудой A периодом T, сдвинутая по оси ОХ на величину 
|
Способы задания функции
Обычно рассматривают три способа задания функции: аналитический, табличный, графический.
- Аналитический способ задания функции
Если функция выражена при помощи формулы, то она задана аналитически.
Например 
Если функция y=f(x) задана формулой, то ее характеристика f обозначает ту совокупность действий, которую нужно в определенном порядке произвести над значением аргумента x, чтобы получить соответствующее значение функции.
Пример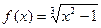 
. Выполняется три действия над значением аргумента.
- Табличный способ задания функции
Этот способ устанавливает соответствие между переменными с помощью таблицы. Зная аналитическое выражение функции, можно представить эту функцию для интересующих нас значений аргумента при помощи таблицы.
Можно ли от табличного задания функции перейти к аналитическому выражению?
Заметим, что таблица дает не все значения функции, причем промежуточные значения функции могут быть найдены лишь приближенно. Это, так называемое интерполирование функции. Поэтому, в общем случае найти точное аналитическое выражение функции по табличным данным нельзя. Однако всегда можно построить формулу, и при том не одну, которая для значений аргумента, имеющихся в таблице, будет давать соответствующие табличные значения функции. Такого рода формула называется интерполяционной.
- Графический способ задания функции
Аналитический и табличный способы не дают наглядного представления о функции.
Этого недостатка лишен графический способ задания функции y=f(x), когда соответствие между аргументом x и функцией y устанавливается с помощью графика.
Понятие неявной функции
Функция называется явной, если она задана формулой, правая часть которой не содержит зависимой переменной.
Функция y от аргумента x называется неявной, если она задана уравнением
F(x,y)=0 (1) неразрешенным относительно зависимой переменной.
Пример. 
Понятие обратной функции
Пусть задана функция y=f(x) (1). Задавая значения аргумента х, получаем значения функции y.
Можно, считая y аргументом, а х – функцией, задавать значения y и получать значения x. В таком случае уравнение (1) будет определять x, как неявную функцию от y. Эта последняя функция называется обратной по отношению к данной функции y.
Предполагая, что уравнение (1) разрешено относительно x, получаем явное выражение обратной функции
(2), где функция 
для всех допустимых значений y удовлетворяет условию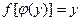 
Пример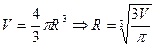 
Замечание
Обратная функция однозначной функции может быть многозначной, то есть данному значению y может соответствовать несколько значений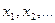 
обратной функции .
Например, тригонометрические функции и обратные тригонометрические функции. Или
- двузначная.
