Лекция 17. Обыкновенные дифференциальные уравнения. Основные понятия. Уравнения с разделяющимися переменными. Однородные уравнения. Линейные уравнения первого порядка.
1. Определение обыкновенного дифференциального уравнения (ОДУ) и его решения. Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной функции y = f (x) и её производных (или дифференциалов):
 ;
| (1) |
(все три переменные x, y, F - действительны).
Опр. Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала).
Пример: y (4)– y + x =0 - уравнение четвёртого порядка.
Опр. Частным решением уравнения (1) на интервале (a, b) (конечном или бесконечном) называется любая n раз дифференцируемая функция 
, удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество.
Так, функция y (x) = ex + x обращает уравнение: y (4) – y + x = 0 в тождество на всей числовой оси (y (4)(x) = ex; ex –(ex + x) + x = 0), т.е. является частным решением этого уравнения. Любое уравнение порядка 
имеет множество частных решений (частным решением приведённого уравнения является и функция y (x) = sin(x) + x). Процедуру решения дифференциального уравнения часто называют интегрированием уравнения, при этом интегрировать приходится в общем случае ровно n раз, и при каждом интегрировании в решение входит очередная произвольная постоянная.
Опр. Общим решением (общим интегралом) уравнения (1) называется такое соотношение
 ;
| (2) |
что: 1. Любое решение (2) 
относительно y (для набора постоянных C 1, C 2, …, Cn из некоторой области n -мерного пространства) - частное решение уравнения (1);
2. Любое частное решение уравнения (1) может быть получено из (2) при некотором наборе постоянных C 1, C 2, …, Cn.
Мы будем в основном рассматривать дифференциальные уравнения в форме, разрешённой относительно старшей производной:
 ;
| (3) |
и получать общее решение в форме
| ;
| (4) |
решённой относительно неизвестной функции.
ОДУ первого порядка.
Как следует из определения, обыкновенным дифференциальным уравнением первого порядка называется уравнение
 ;
| (5) |
где x - независимая переменная, y (x) - неизвестная функция. В форме, разрешённой относительно производной, уравнение первого порядка записывается так:
 ;
| (6) |
Если пользоваться другим обозначением производной, то можно записать (6) как
 ;
| (7) |
Общее решение (общий интеграл) уравнения при n = 1 имеет вид 
или 
.
3. Геометрический смысл уравнения первого порядка. Уравнение (6) в каждой точке (x, y) области D, в которой задана функция f (x, y), определяет 
- угловой коэффициент касательной к решению, проходящему через точку (x, y), т.е. направление, в котором проходит решение через эту точку. Говорят, что уравнение (6) задаёт в D поле направлений. График любого решения дифференциального уравнения (называемый также интегральной кривой) в любой своей точке касается этого поля, т.е. проходит в направлении, определяемом полем. Интегрирование дифференциального уравнения геометрически означает нахождение кривых, у которых направление касательной в каждой точке совпадает с направлением поля. На рисунке справа изображено поле направлений, определяемое уравнением 
, и три интегральные кривые (три частных решения) этого уравнения. Решение можно провести через любую точку области D; единственное решение можно выделить, если задать точку, через которую проходит интегральная кривая:
.
Для изображения поля направлений, задаваемого дифференциальным уравнением, рассматривают линии уровня функции f (x, y), т.е. геометрические места точек, в которых касательные к интегральным кривым сохраняют постоянное направление. Такие линии называются изоклинами. С помощью изоклин можно приближённо изобразить интегральные кривые.
Для примера построим изоклины уравнения 
. Перебираем различные значения постоянной C, строим линии уровня функции 
, соответствующие этим значениям С (т.е. прямые 
), и на этих линиях ставим чёрточки в направлении, определяемым значением С (
, где 
- угол между чёрточкой и положительным направлением оси Ох): 
- ось Оу; 
; 
; 
и т.д. Информация о направлении интегральных кривых, полученная из рисунка (выше справа), достаточна, чтобы сделать качественный вывод об их поведении: кривые должны огибать начало координат. Это могут быть окружности или спирали (когда мы научимся решать дифференциальные уравнения, мы легко установим, что это окружности; две такие окружности изображены пунктиром).
4. Задача Коши (задача с начальным условием). Пусть функция f (x, y) определена в области D, точка 
. Требуется найти решение уравнения
| ;
| (8) |
удовлетворяющее начальному условию
| y (x 0) = y 0;
| (9) |
(начальное условие (9) часто записывают в форме ).
Теорема Коши (существования и решения задачи Коши). Если в области D функция f (x, y) непрерывна и имеет непрерывную частную производную 
, то для любой точки в окрестности точки x 0 существует единственное решение задачи ((8),(9)).
Мы примем эту теорему без доказательства. На самом деле для существования решения в окрестности точки x 0 достаточно только непрерывности функции f (x, y); условие непрерывности обеспечивает единственность этого решения. 6
Уравнения с разделяющимися переменными.
Уравнения с разделёнными переменными.
Так называются уравнения вида (10), удовлетворяющее начальному условию
| f (x) dx + g (y) dy = 0.
| (10) |
Пусть y (x) - решение этого уравнения, т.е. f (x) dx + g (y (x)) dy (x) = 0. Интегрируя это тождество, получим 
- общий интеграл (общее решение) этого уравнения.
Пример: решить задачу Коши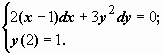 
Исходное уравнение - с разделёнными переменными, интегрируя его, получим 
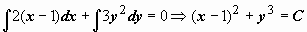. Соотношение (x -1)2 + y 3 = C - общее решение (общий интеграл) уравнения; для того, чтобы найти частное решение, удовлетворяющее начальному условию, надо подставить в общее решения данные значения x 0 и y 0, и найти значение постоянной C на этом решении: (2-1)2 + 13 = 2 
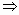C = 2. Таким образом, решение поставленной задачи: (x -1)2 + y 3 = 2.
Уравнения с разделяющимися переменными. Так называются уравнения вида
 или
| (11) |
| f 1(x) g 1(y) dx + f 2(x) g 2(y) dy = 0
| (12) |
Эти уравнения легко сводятся к уравнению с разделёнными переменными:
Записываем уравнение (11) в форме  , затем делим на g (y) и умножаем на dx:  .
| Уравнение (12) делим на f 2(x)g  (y)  g 1(y):  .
| ||
| Эти уравнения - с разделёнными переменными. Интегрируя, получим общие интегралы: | |||
 .
|  .
| ||
| В обоих случаях возможна потеря решений: деление на функцию может привести к уравнению, которое неэквивалентно данному. | |||
| Если функция g (y) имеет действительные корни y 1, y 2, y 3, …, то функции y = y 1, y = y 2, y = y 3, …, очевидно, являются решениями исходного уравнения. | Если функция f 2(x) имеет действительные корни x 1, x 2, x 3, …, функция g 1(y) имеет действительные корни y 1, y 2, y 3, …, то функции x = x 1, x = x 2, x = x 3, …, y = y 1, y = y 2, y = y 3, … являются решениями исходного уравнения. | ||
| В обоих случаях эти решения могут содержаться в общем решении, но могут и не содержаться в нём; последнее может случиться, если на этих решениях нарушаются условия теоремы существования и единственности решения задачи Коши.
| |||
Примеры:
1. 
.
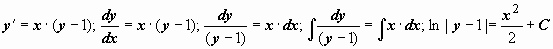При такой форме записи общего интеграла решение y = 1 потеряно. Можно преобразовать общее решение к виду, который содержит это решение. Переобозначим постоянную C как ln| C 1|: 
. Вернёмся к обозначению постоянной интегрирования C; общее решение 
содержит частное решение y = 1 при C = 0.
2. Найти решение задачи Коши 
Решаем уравнение: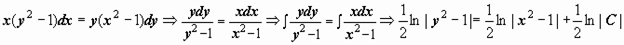 
. Здесь могут быть потеряны решения 
постоянная интегрирования записана как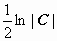 
. Далее, 
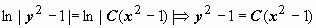. Общий интеграл уравнения y 2 = C (x 2 – 1) + 1. Частные решения 
содержатся в общем интеграле при C = 0, решения 
утеряны (понятно, почему это произошло: если записать уравнение в форме, решённой относительно производной, 
, то, очевидно, на решениях нарушаются условия, налагаемые теоремой Коши на правую часть уравнения). Всё множество решений: y 2 = C (x 2 – 1) + 1, x = 1, x = -1. Мы должны найти ещё частное решение, удовлетворяющее начальному условию y (1) = 5. Подстановка значений x = 1, y = 5 в общий интеграл даёт 25=1, т.е. общий интеграл этого частного решения не содержит. Решение x = 1 удовлетворяет начальному условию, это и есть решение задачи Коши.
К уравнениям с разделяющимися переменными сводятся уравнения вида 
(
- постоянные). Если перейти к новой неизвестной функции z = ax + by + c, то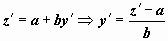 
, и уравнение представляется как 
. Это - уравнение с разделяющимися переменными.
Пример: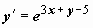 
. 
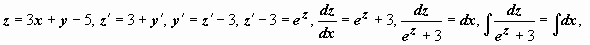
6. Уравнения с однородной правой частью. Так называются уравнения со специальным видом зависимости функции f (x, y) от своих аргументов:
 .
| (13) |
Это уравнение сводится к уравнению с разделяющимися переменными относительно новой неизвестной функции u (x) заменой 
, или 
. Подставляя в (13) y = x · u, y ′ = u + x · u ′, получим 
(это - уравнение с разделяющимися переменными), 
- это общий интеграл уравнения относительно переменных x, u.
Пример: 
- общее решение уравнения.
Как "узнать в лицо" уравнение с однородной правой частью? Введём определение. Функция f (x, y) называется однородной функцией своих аргументов степени m, если для любого t выполняется тождество f (tx, ty) = tm f (x, y). Так, x 3 – 3 xy 2 + 4 y 3 - однородная функция степени 3, ln x – ln y - однородная функция нулевой степени. Если M (x, y), N (x, y) - однородные функции одной степени, то уравнение M (x, y) dx + N (x, y) dy = 0 может быть приведено к виду .
Примеры: 1. (y 2 - 2 xy) dx + x 2 dy = 0. Здесь коэффициенты при дифференциалах - однородные функции второй степени, т.е. уравнение должно приводиться к виду (13). Решаем уравнение относительно производной: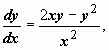 
делим числитель и знаменатель правой части на x 2: 
- это уравнении с однородной правой частью. 
Это общий интеграл уравнения. Утерянные решения: x = 0, y = x (u = 1); решение y = 0 (получаемое из u = 0) содержится в общем решении при C = 0.
2. 
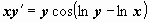. Преобразуем уравнение: 
. Решение: 
общий интеграл уравнения в переменных x, u: 
. Преобразуем это выражение: 
, или 
(
). Утерянные решения: 
Ответ: (); .
7. Линейные уравнения. ДУ первого порядка называется линейным, если неизвестная функция y (x) и её производная входят в уравнение в первой степени:
 .
| (14) |
Здесь p (x), q (x) - непрерывные функции.
Для решения уравнения (14) представим y (x) в виде произведения двух новых неизвестных функций u (x) и v (x): y (x) = u (x) v (x). Тогда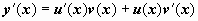 
, и уравнение приводится к виду 
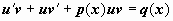, или 
. Это уравнение решаем в два этапа: сначала находим функцию v (x) как частное решение уравнения с разделяющимися переменными 
; затем находим u (x) из уравнения 
. Итак, 
(мы не вводим в это решение произвольную постоянную C, нам достаточно найти одну функцию v (x), обнуляющую слагаемое со скобками в уравнении ). Теперь уравнение для u (x) запишется как 
. Общее решение уравнения (14):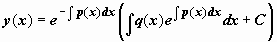 
.
Пример. 
.
Решение: 
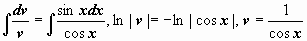. Теперь для u (x) получим: 
, и общее решение уравнения 
. Для нахождения частного решения, соответствующего начальным условиям задачи Коши, подставим в общее решение 
. Решение задачи: 
.
Этот метод решения линейных уравнений часто реализуется по-другому - в форме вариации произвольной постоянной. Уравнение (14) называется однородным, если q (x) = 0. Пусть дано неоднородное уравнение (14) 
. Оно, как и в предыдущем случае, решается в два этапа. Обнулим правую часть, получившееся уравнение будем называть однородным уравнением, соответствующим уравнению (14): 
. Решаем это уравнение: 
(при делении на y теряется решение y (x) = 0, но оно входит в общее решение при C = 0). Теперь ищем общее решение уравнения (14) в ви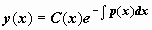де 
, где 
- новая неизвестная функция; находим производную 
и подставляем в (14) y и 
: 
, или 
, где 
. Теперь 
.
Понятно, что обе реализации решения имеют один смысл (решение однородного уравнения играет роль функции v (x), варьируемая постоянная C (x) - роль функции u (x)).
Отметим ещё одно важное обстоятельство. Переменные x и y равноправны, поэтому надо иметь в виду, что можно искать решение в виде x = x (y), а не в виде y = y (x).
Пример: (x + y 2) dy = ydx. Если представить его в виде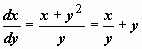 
, то относительно функции x = x (y) оно линейно. Решаем его методом вариации произвольной постоянной. Соответствующее однородное уравнение: 
. Его решение: 
. Ищем решение данного уравнения в форме x = C (y) y. Тогда 
(постоянная C 0 переобозначена как 
). Утерянное решение - y = 0.
