В твердой среде
Пусть в однородной и изотропной упругой твердой среде в направлении оси 0 х распространяется продольная плоская волна. Выделим в среде цилиндрический объем с площадью основания S и высотой Δ х (рис. 4.1).
Смещения u частиц, как было показано ранее (рис. 8), являются функциями координаты х, поэтому смещения частиц на основаниях цилиндра с координатами х и х +Δ х, соответственно, будут u и u +Δ u. Выделенный объем цилиндра либо растягивается, либо сжимается в зависимости от знака абсолютной деформации Δ u (Δ u > 0 – деформация растяжения и Δ u < 0 – деформация сжатия). Величина средней относительной деформации (растяжение или сжатие, приходящаяся на единицу длины цилиндра) равна Δ u /Δ х. Поскольку u не является линейной функцией х (рис. 4.2), она остается зависящей от х - истинная относительная деформация в разных сечениях цилиндра будет неодинаковой. Чтобы получить относительную деформацию u в сечении х, нужно перейти к пределу Δх→0 и записать
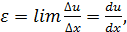(4.1)
где мы ввели символ частной производной, поскольку абсолютная деформация u является функцией двух переменных – координаты х и времени t
u = u (x, t)
| х |
| х +Δ х |
| u +Δ u |
| S |
| u |
| σ(х +Δ х + u +Δ u) |
| σ(х + u) |
| х |
| Рис. 4.1. Упругая волна в твердой среде |
Процедура введения истинного значения относительной деформации ε в данной точке среды аналогична процедуре введения понятия мгновенной скорости, когда ставится задача определения скорости точки в данный момент времени
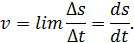
| du / dx =0 |
| du / dx >0 |
| du / dx <0 |
| x |
| u |
| Рис. 4.2. Производная деформаций |
Наличие продольных деформаций свидетельствует о существовании нормального напряжения σ, для малых деформаций, в соответствии с законом Гука, пропорционального величине относительной деформации du / dx:
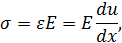
где Е – модуль Юнга данной среды.
Закон Гука: деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. п.), пропорциональна приложенной к этому телу силе.
Следует отметить, что закон Гука выполняется только при малых деформациях. При превышении некоторого предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для некоторых сред закон Гука неприменим даже при малых деформациях.
Модуль Юнга (модуль продольной упругости) – физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации. Назван в честь английского физика XIX века Томаса Юнга. В Международной системе единиц (СИ) измеряется в ньютонах на метр в квадрате (н/м2) или в паскалях (Па).
Модуль Юнга рассчитывается следующим образом:
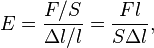
где:
- F - нормальная составляющая силы;
- S - площадь поверхности, по которой распределено действие силы,
- l - длина деформируемого стержня,
- 
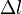- модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l).
Значения модуля Юнга для некоторых материалов приведены в табл. 4.1.
Отметим, что относительная деформация du / dx, а, следовательно, и напряжение σ в фиксированный момент времени зависит от х (рис. 4.2). Там, где отклонения частиц от положения равновесия максимальны, деформация и напряжения равны нулю (тангенс угла наклона касательной, которая представляет собой производную du / dx, равна нулю). В местах, где частицы проходят через положения равновесия, относительные деформации и напряжения достигают максимальных значений, причем положительные и отрицательные деформации (растяжения и сжатия) чередуются друг с другом (производная du / dx в этих точках меняет знак: касательные в этих точках составляют либо острый, либо тупой угол с осью 0 х). В соответствии с этим продольная волна состоит из чередующихся разрежений и сжатий среды.
Таблица 4.1
