Симплексный метод – это метод целенаправленного перебора опорных решений задачи ЛП.Он позволяет за конечное число шагов либо найти оптимальное решение, либо установить, что его не существует. Основное содержание метода состоит в следующем:
1. Указать способ нахождения начального опорного плана.
2. Указать способ перехода от одного опорного плана к другому, на котором значение целевой функции ближе к оптимальному.
3. Задать критерии, которые позволяют своевременно прекратить проверку решений на оптимальность или сделать заключение об отсутствии оптимального решения.
Предположим, что необходимо найти минимум целевой функции 
при следующей системе ограничений:
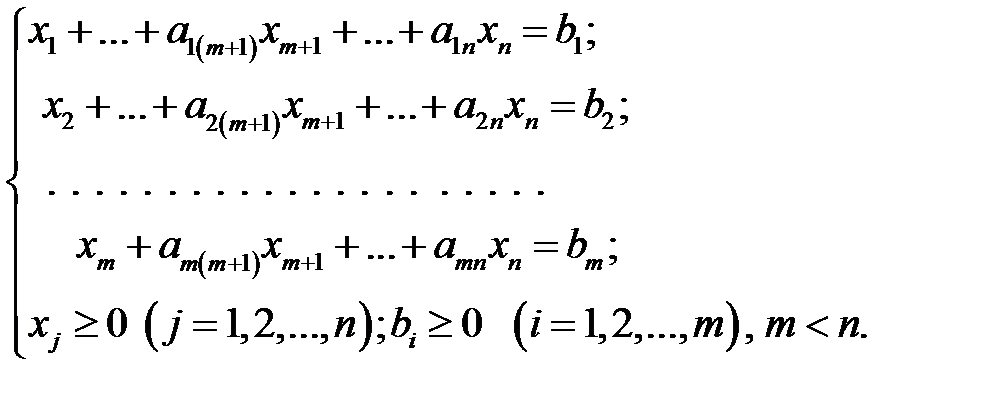(1.14)
Запишем систему (1.14) в векторной форме:
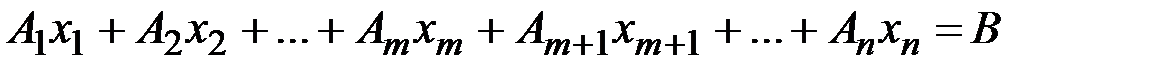(1.15) 
, 
,…,, 
, 
,..., 
.
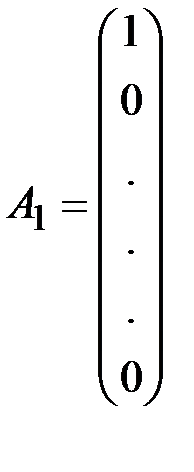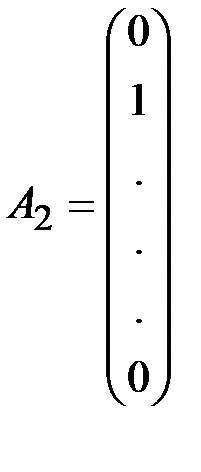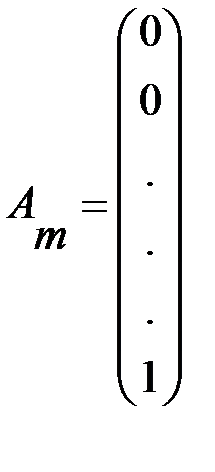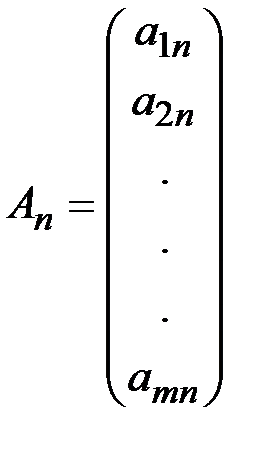Векторы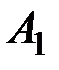 
, 
,.., 
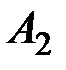образуют базис в 
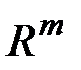. Поэтому в соотношении (1.15) за базисные переменные принимаем 
, 
,…, 
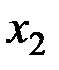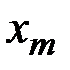, а остальные переменные
(будем называть их свободными) приравниваем нулю. Учитывая, что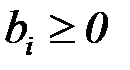 
, получаем, что опорное решение задачи (1.14)имеет вид
Рассмотрим, как, исходя из начального опорного решения, можно построить другое опорное решение, которое будет более близким к оптимальному, т.е. на котором значение целевой функции будет меньше. Систему ограничений (1.14) перепишем в виде:
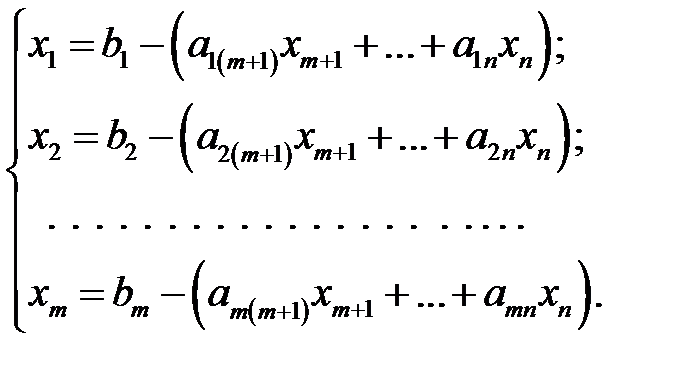(1.16)
Выражая значения , ,…, 
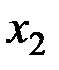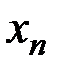через свободные неизвестные, целевую функцию 
получим в виде:
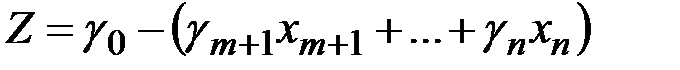. (1.17)
Итак, первоначальный опорный план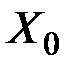 
, а соответствующее значение 
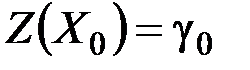. Возможны следующие ситуации:
1) все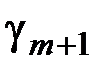 
, 
, …, 
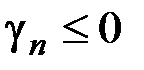. Тогда минимум 
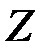достигается при 
, т.е. план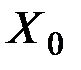 
является оптимальным и 
;
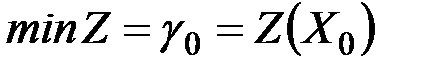2) среди чисел , , …,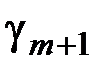 
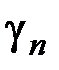имеются положительные. Пусть 
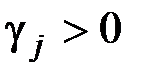, где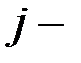 
одно из чисел 
, 
,..;, 
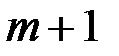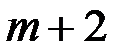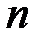. Тогда полагаем все 
, 
, …, 
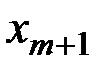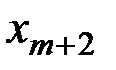равными нулю, кроме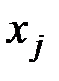 
. Из (1.16) следует, что
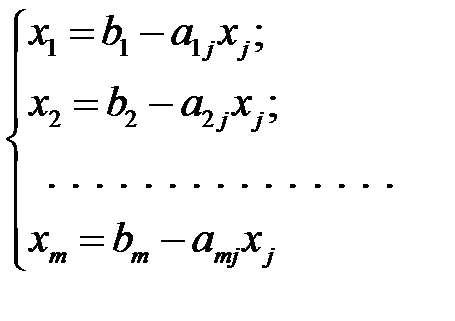(1.18)
и 
.
Здесь, в свою очередь, могут представиться два случая:
а) все числа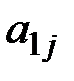 
, 
, …, 
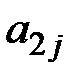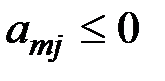, тогда для любого 
все значения , ,…, 
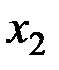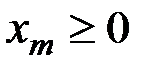. В этом случае 
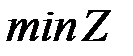не достигается, так как при 
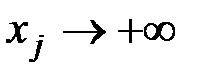функция 
;
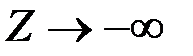б) среди чисел , , …,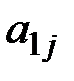 
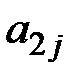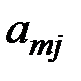имеются положительные. Пусть, например, 
. Так как все компоненты плана должны быть положительны, то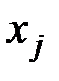 
нельзя увеличивать более, чем 
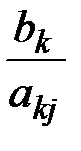(иначе 
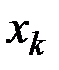станет отрицательным).
Поэтому найдём 
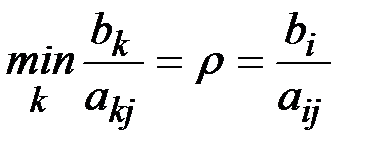
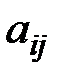называется разрешающим элементом. Положим 
,…, 
, 
, 
,…, 
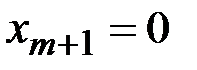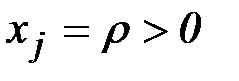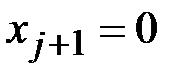. Найдём значения остальных неизвестных:
Получено новое опорное решение: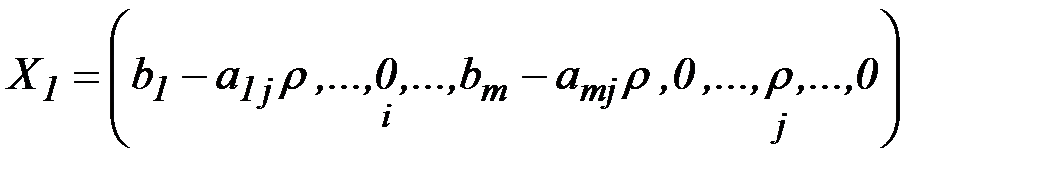 
.
Значение целевой функции при этом уменьшается:
.
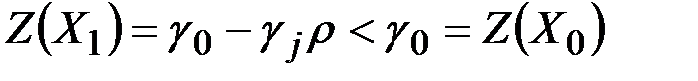Идея симплекс-метода заключается в том, что на каждом этапе один из векторов 
выводится из базиса, а вместо него вводится другой 
. При этом удобно, чтобы он стал бы единичным. Поэтому в системе ограничений 
-е уравнение, содержащее разрешающий элемент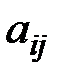 
, делим на 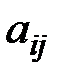. Исключаем 
из всех остальных уравнений, т.е. осуществляем преобразование Жордана-Гаусса.
Итак, алгоритм симплекс-метода состоит в следующем:
1. Приводим систему к виду, содержащему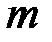 
единичных векторов, и определяем первоначальный опорный план.
2. Выражаем 
через свободные переменные в виде:
.
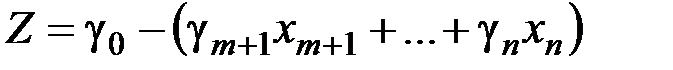Если при этом все коэффициенты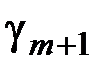 
, 
,.., 
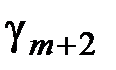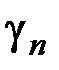не являются положительными, то найденный первоначальный план является оптимальным.
3. Пусть среди чисел 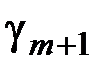, ,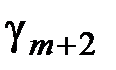.., 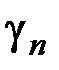имеются положительные. Берём любой из них, например, 
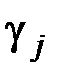, и просматриваем весь соответствующий столбец 
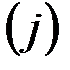. Он называется разрешающим столбцом. Если все числа этого столбца отрицательны, то 
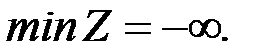Задача решения не имеет.
4. Если в этом столбце есть положительные числа, то находим разрешающий элемент – это элемент, для которого отношение 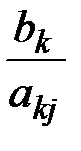минимально. Пусть это элемент 
.
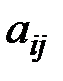5. Выводим переменную 
из числа свободных и меняем её с базисной переменной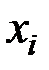 
.
6. Эту процедуру выполняем до тех пор, пока все коэффициенты при свободных неизвестных станут неположительными, (это признак оптимальности плана) либо неположительными станут все элементы в разрешающем столбце (т.е.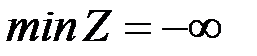 
).
Замечание 1. На практике этот алгоритм реализуется с помощью симплекс-таблиц (см. пример 1.2.).
Замечание 2. При построении симплекс-таблиц можно рассуждать иначе. Пусть решаем ЗЛП в виде
,
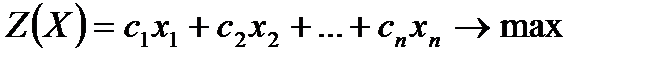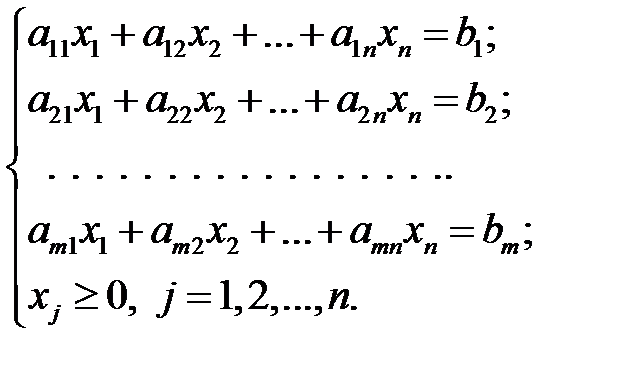
В этом случае общая схема симплекс-метода претерпевает некоторые изменения. А именно:
1) Пусть дан базис некоторого опорного решения и соответствующая ему симплекс-таблица. В верхней строке этой таблицы (см. пример 1.2., заголовки столбцов) располагаются свободные переменные, в крайнем левом столбце – базисные переменные; крайний правый столбец – это столбец свободных членов, а самая нижняя строка является строкой целевой функции и называется вектором относительных оценок. Остальное содержимое таблицы - столбцы матрицы ограничений, отвечающие соответствующим столбцам свободных переменных. Координаты вектора относительных оценок (D1, D2,… Dn) находят по правилу: для нахождения коэффициента Dk вектор из коэффициентов при базисных переменных в целевой функции скалярно умножить на k -й столбец симплекс-таблицы и вычесть из найденного числа коэффициент целевой функции при соответствующем свободном переменном xk.
2) Если все относительные оценки (нижняя строка этой таблицы) неотрицательны, то построено оптимальное опорное решение.
3) Если существует отрицательная оценка и соответствующий ей столбец (разрешающий) состоит из неположительных элементов, то имеет место неразрешимость целевой функции Z (X), то есть max Z (X) ®+¥.
4) Иначе, выбрать ведущий элемент (задаёт ведущую строку) и сделать с ним шаг жордановых исключений, перейдя к новой симплекс-таблице, которую проанализировать как в пункте 2).
Пример 1.2. Предприятие, выпускающее продукцию на экспорт, располагает тремя производственными ресурсами (сырьем, оборудованием, электроэнергией) и может организовать производство продукции двумя различными способами. Расход ресурсов и амортизация оборудования за один месяц и общий ресурс при каждом способе производства заданы в таблице (в ден. ед.).
| Производственный ресурс | Расход ресурсов за 1 месяц и общий ресурс при работе | Общий ресурс | |
| по 1 способу | по 2 способу | ||
| Сырье | |||
| Оборудование | |||
| Электроэнергия |
При первом способе производства предприятие выпускает за один месяц 3 тыс. изделий, при втором – 4 тыс. изделий.
Сколько месяцев должно проработать предприятие по каждому из этих способов, чтобы при наличных ресурсах обеспечить максимальный выпуск продукции?
Решение. Обозначим:
- время работы предприятия по первому способу;
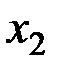- время работы предприятия по второму способу.
Математическая модель задачи примет вид:
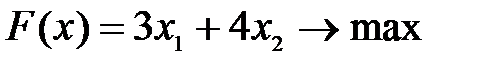
при ограничениях:
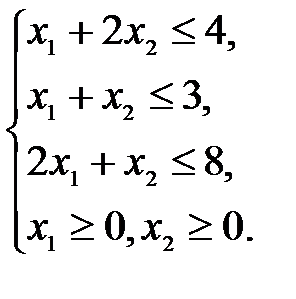
Приведем задачу к каноническому виду:
при ограничениях:
Принимаем 
, 
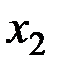в качестве свободных переменных, 
, 
, 
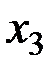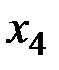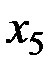в качестве базисных. Составляем симплекс-таблицу (в сокращённой форме), соответствующую начальному опорному плану. Обратим внимание, что коэффициенты при свободных переменных пишутся с противоположным знаком.
 
| 
| 
| 
|
| |||
| |||
| |||
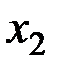
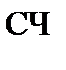
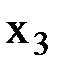
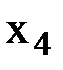
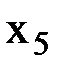
| -3 | -4 |
Начальный опорный план имеет вид:
В последней строке имеются две отрицательные оценки, значит, найденное решение не является оптимальным и его можно улучшить. В качестве ведущего столбца следует принять столбец базисной переменной 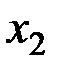, а за ведущую строку – строку переменной 
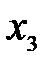, где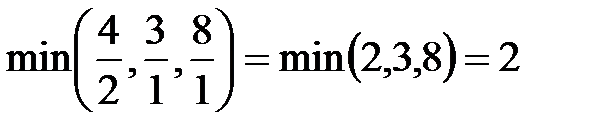 
.
Теперь запишем правила перехода к новой симплекс-таблице, соответствующие приведённому выше алгоритму симплекс-метода:
1. Базисная переменная, находящаяся в ведущей строке, и свободная переменная, находящаяся в ведущем столбце, меняются местами.
2. Ведущий элемент заменяется величиной, ему обратной.
3. Все элементы ведущей строки (включая свободный член), кроме ведущего элемента, заменяются их отношениями к ведущему элементу.
4. Все элементы ведущего столбца (кроме ведущего элемента) заменяются взятыми с обратными знаками их отношениями к ведущему элементу.
5. Остальные элементы заменяются по «правилу 4 элементов»: любой такой элемент умножается на ведущий и из произведения вычитается произведение двух других элементов, составляющих с первыми вершины прямоугольника, после чего результат делится на ведущий элемент.
Ведущим элементом является «2». Вводим в столбец БП переменную 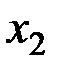, выводим 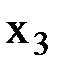. Составляем симплексную таблицу второго шага:
|
|
|
|
|
|
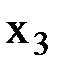
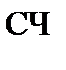
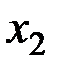
| 1/2 | 1/2 | |
|
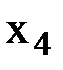
| 1/2 | -1/2 | |
|
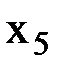
| 3/2 | -1/2 | |
|
| -1 |
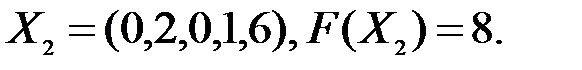
В последней строке имеется одна отрицательная оценка. Полученное решение можно улучшить. Ведущим элементом является «1/2». Составляем симплекс таблицу третьего шага:
|
|
|
|
|
|
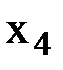
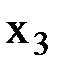
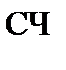
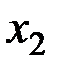
| -1 | ||
|
| -1 | ||
|
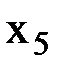
| -3 | ||
|
|
Все оценки свободных переменных положительны, следовательно, найденное опорное решение является оптимальным:
Ответ. Максимальный выпуск продукции составит 10 тыс. ед., при этом по первому способу предприятие должно работать два месяца, по второму – один месяц.
