В тех случаях, когда в задаче ЛП лишь две переменные, можно использовать для решения графический метод. Пусть требуется найти максимальное (минимальное) значение функции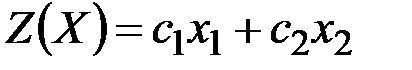 
при ограничениях:
(1.5)
Данный метод основывается на возможности графического изображения области допустимых решений задачи, т.е. удовлетворяющих системе (1.5), и нахождения среди них оптимального решения. Область допустимых решений задачи строится как пересечение (общая часть) областей решений каждого из заданных ограничений (1.5). Каждое из них определяет полуплоскость с границей 
, 
. Для того, чтобы определить, какая из двух полуплоскостей является областью решений, достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство: если оно удовлетворяется, то областью решений является полуплоскость, содержащая данную точку, если же неравенство не удовлетворяется, то областью решений является полуплоскость, не содержащая данную точку.
Пересечение этих полуплоскостей образует некоторую область, называемую многоугольником решений, который является выпуклым множеством. (Допустим, что система ограничений совместна, а многоугольник её решений ограничен.) Для нахождения среди допустимых решений оптимального используются линии уровня и опорные прямые.
Линией уровня называется прямая, на которой целевая функция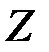 
принимает постоянное значение. Уравнение линии уровня имеет вид
, где 
.
Все линии уровня параллельны между собой. Их нормаль 
.
Опорной прямой называется линия уровня, которая имеет хотя бы одну общую точку с областью допустимых решений, по отношению к которой эта область находится в одной из полуплоскостей (рис. 1).
Рис. 1.1
Значения 
возрастают в направлении вектора 
. Поэтому необходимо передвигать линию уровня 
в направлении этого вектора параллельно самой себе до опорной прямой L 1в задаче на максимум и в противоположном направлении – в задаче на минимум (до опорной прямой L 2).
Приведём решение примера 1.1. Напомним, что нужно найти максимум функции 
при ограничениях
Решение. Строим область допустимых решений. Нумеруем ограничения задачи. В прямоугольной декартовой системе координат (рис.1.2) строим прямую 
, соответствующую ограничению (1). Находим, какая из полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1).
Для этого достаточно координаты какой - либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая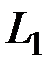 
не проходит через начало координат, подставляем 
в первое ограничение 
. Получим строгое неравенство 
. Следовательно, точка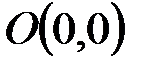 
лежит в полуплоскости решений. Аналогично строим прямую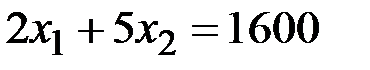 
и область решений ограничения (2). Находим общую часть полуплоскостей решений, учитывая ограничения (3). Полученную область допустимых решений выделим на рис.1.2 тёмным цветом.
Рис.1.2
Строим линию уровня 
и вектор 
, который указывает направление возрастания функции 
и перпендикулярен прямой 
. Линию уровня 
перемещаем параллельно самой себе в направлении 
до опорной прямой. Получим, что максимума целевая функция достигнет в точке 
точке пересечения прямых 
и 
. Решая систему из уравнений этих прямых 
, получим координаты точки 
. Следовательно, 
, а 
, 
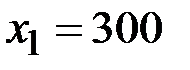оптимальное решение.
