Простые и дифференциальные цепи металлорежущих станков.

Простой кинематической цепью назы­вается такая цепь, у которой от од­ного конечного звена к другому передается только одно движение, на­пример, у винторезной цепи (см. рис. 9) от шпинделя к суппорту передается только одно движение (при данной на­ладке).

Уравнение баланса простой винторез­ной цепи:

(1)

Дифференциальной кинематической цепью называется такая, которая сообщает до­полнительное движение конечному звену кинематической цепи. В результате на этом звене суммируются два движе­ния. Рассмотрим, как изменяется стуктура кинематической цепи, если простую цепь преобразовать в дифференциальную.

Для этого преобразуем простое уравнение ба­ланса винторезной цепи (1) в диффе­ренциальное уравнение баланса путем замены i_x суммой:

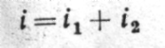
Подставим последнее выражение в уравнение баланса (1), получим:

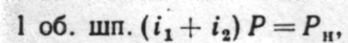(2)

где Р — шаг ходового винта; Рн— шаг нарезаемой резьбы.

Уравнение (2) есть уравнение балан­са дифференциальной винторезной це-

пи, так как левая его часть пред­ставляет сумму. Построим по уравне­нию (2) кинематическую цепь (рис. 23). Из кинематической цепи видно, что перемещение гайки 2 ходового винта, а следовательно, и перемещение суппор­та 1 вдоль станка складывается из поворота ходового винта и поворота гайки 2. Настройку вращения на обо­роты ходового винта осуществляют ги­тарой i_y, а ходового валика 3 и гай­ки 2 — i_x. Наличие двух неизвестных в одном уравнении может дать беско­нечно большое число решений, поэто­му дифференциальные цепи имеют боль­ший диапазон настройки, чем простые, и делают станок более универсальным.

Станки с дифференциальными кине­матическими цепями используются для обработки деталей, образованных сложными поверхностями, например, для нарезания цилиндрических колес с косыми зубьями, затылования червяч­ных фрез и т. д. Обработка таких поверхностей требует осуществления сложных настроек кинематических це­пей. Таким образом, дополнительную диф­ференциальную кинематическую цепь вводят для обеспечения точных настроек станка. В данном случае (рис.23) при работе станка на заготовке (инструменте) происходит суммирование двух движений. В зубофрезерных станках при обработ­ке цилиндрических колес с косыми зубьями на заготовке также суммируются два движения: от инструмента (чер­вячной фрезы) на заготовку, через гитару обкатки и от ходового винта через гитару дифференциальной цепи.

Дифференциальные цепи значитель­но расширяют диапазон и точность настроек станков.

 

6. Настройка кинематических цепей.

При настройке кинематических цепей металлорежущих станков всегда дви­жение одного конечного звена цепи строго координируется с другим ко­нечным звеном. В одних случаях тре­буется абсолютная точность в согла­совании движений, в других — допуска­ется некоторая погрешность и согласование движений может быть лишь приближенным. Поэтому, прежде чем приступить к настройке станка, необхо­димо выяснить, какие именно движения следует сообщить обрабатываемой де­тали и инструменту и какая зависи­мость должна быть между этими движениями. Независимо от слож­ности станка методика кинематиче­ской настройки во всех случаях оди­накова и состоит в подборе сменных зубчатых колес гитар. Для решения задач по наладке кинематических це­пей предложен ряд методор подбора сменных колес гитар. Их можно разде­лить на точные и приближенные.

Точная настройка. Точный метод подбора сменных колес состоит в том, что числитель и знаменатель переда­точного отношения гитары, представ­ленного простой дробью, разлагают на простые множители, а затем умноже­нием (делением) числителя и знамена­теля на одно и то же число образуют числа зубьев сменных колес:

 

Иногда не удается осуществить точ­ный подбор сменных колес нормаль­ного комплекта, поэтому применяют приближенные способы подбора, кото­рые могут обеспечить заданную точность шага нарезаемой резьбы.

Приближенная настройка. Рассмот­рим способ прибавления (вычитания) малых чисел к передаточному отно­шению. При этом способе к числителю и знаменателю передаточного отноше­ния прибавляют (или вычитают) число, удобное для разложения на простые множители.

Пусть передаточное отношение гита­ры 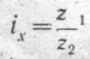но,z₁, и z₂ такие числа,

которые не соответствуют числам зубь­ев сменных колес нормального комп­лекта, следовательно, точная настрой­ка гитары невозможна. Производим приближенную настройку. Для этого прибавляем к числителю и знамена­телю малое число с и получаем новое,

приближенное передаточное отношение причем i_x1близко по сво­ему значению к i_x.

 

 

Установим, от чего зависит величи­на погрешности приближенной настрой­ки. Для этого исследуем разность пере­даточных отношений:

 

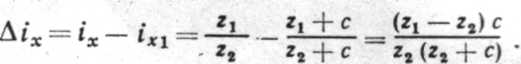
.Следовательно, чтобы ошибка была минимальной, с=1, a z₁, и z₂ близки по своему значению друг к другу, т. е. ', тогда

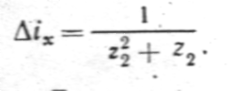
Таким образом, метод прибавления или вычитания малых чисел пригоден в том случае, когда передаточное от­ношение близко к единице или возмож­но преобразовать передаточное отно­шение так, чтобы часть его представ­ляла отношение, близкое к единице. Этот способ удобен при подборе смен­ных колес в три пары.

При анализе погрешности настройки определяют абсолютную, относитель­ную и суммарные погрешности. Абсо­лютная погрешность Δi_х есть разность между полученным i_xl и заданным i_x передаточными отношениями. Отно­сительная погрешность δ есть отно­шение абсолютной погрешности к за­данному передаточному отношению.

Суммарная погрешность ΔL приближенной настройки есть произведение относительной погрешности б на длину
L обрабатываемой детали.,

Подбор сменных зубчатых колес производят по таблицам М. Н. Петрик и В. А. Шишкова. По табли­цам сравнительно просто и с большой точностью можно подобрать сменные колеса гитар. В них непосредственно указаны числа зубьев ведущих и ведо­мых пар зубчатых колес. При этом для подавляющего числа случаев настройки достаточно применять 29 зубчатых колес с числами зубьев 23, 25, 30, 33, 37, 40, 41, 43, 45, 47, 50, 53, 55, 58, 60, 61, 62, 65, 67, 70, 73, 79, 83, 85, 89, 92, 95, 98, 100.

В таблицах для подбора сменных колес передаточное отношение выражено десятичной дробью с точностью до 10^-7. По ним находят число, близкое к полученному, и с правой стороны, выписывают числа зубьев сменных ко­лес. Если заданное передаточное от­ношение выражено правильной дробью, т. е. числитель меньше знаменателя, первую пару зубчатых колес, данную в таблице, считают ведущей. Если же дробь неправильная, то ее перевора­чивают, переводят в десятичную дробь с точностью до 10^-7, находят по таб­лицам число, близкое к полученному, и с правой стороны выписывают числа зубьев смежных колес, при этом ведущи­ми считают вторые два колеса.

 

 

Делительные механизмы.

Делительные механизмы предназна­чены для кругового и продольного деления при обработке деталей машин и приборов, например зубчатых колес, делительных лимбов, линеек и т. п. К делительным механизмам относят де­лительные приспособления, головки и машины.

:

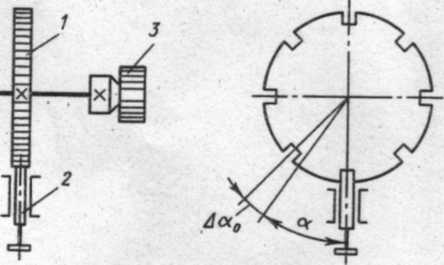
Рис. 25. Приспособление для кругового деления:

1— лимб; 2 — фиксатор; 3 — деталь

Делительныеприспособления-это механизмы непосредственного деления, при котором ошибка между дели­тельными отверстиями лимба целиком переносится на обрабатываемую де­таль. Их применяют, когда нет необ­ходимости в точном делении, например при обработке граней головок бол­тов. На рис. 25 показано приспособ­ление для кругового деления. Погреш­ность деления лимба Δα₀(α— угол поворота лимба и детали) будет переда­ваться на погрешность поворота детали, Δα т. е.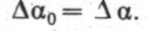

 

[ЛР1]???