Попередні десятиріччя кінця ХХ століття і текучий час характеризувалися широким впровадженням ПЕОМ в практику підрахунку запасів нафти і газу. З одного боку, задача автоматизації підрахунку запасів розглядаються як частина більш складної проблеми, пов’язаної з автоматизацією проектування розробки нафтових і газових родовищ і обґрунтування коефіцієнта вилучення нафти. Багатоваріантні розрахунки технологічних показників розробки базуються на диференціації запасів по площі і розрізу. З другого боку, при підрахунку запасів узагальнюється значний фактичний матеріал по петрографічному, геофізичному і геолого – промисловому вивченню родовищ (покладів) нафти і газу і на основі цього створюється статистичні і динамічні моделі покладів. За допомогою ПЕОМ забезпечується не тільки обробка і систематизація цих даних, але і їх накопичення та зберігання.
В свою чергу автоматизація робіт по створенню гірничо – геометричних моделей покладів і проведення на їх основі підрахунку запасів сприяло створенню потужного апарату математичного забезпечення цих робіт.
Основна увага приділяється геометризації покладів на основі якої здійснюється диференційований підрахунок запасів. Геометризиція покладів передбачає картування різних параметрів в межах покладів шляхом відновлення зміни полів цих параметрів. Поля кожного параметра виражається у вигляді матриці його значень, які задані щільною прямокутною сіткою точок, прообразом якої є полетка П.К. Соболевського. Всі параметри, які визначають запаси нафти і газу у відповідності до формул об’ємного методу, поділяються на арифметичні (числові) і логічні. До числових параметрів відноситься: товщина пласта; коефіцієнти відкритої пористості; нафта – (газо) нафтонасиченості і перерахункові; густина нафти в поверхневих умовах та ін. Серед логічних параметрів виділяються нафтова, газова, водонафтова зони та ін.; зони розповсюдження не колекторів і колекторів, а серед останніх – зони високопродуктивних або низькопродуктивних.
Карти в ізолініях, які уявляють собою графічне зображення відновлених полів геологічних параметрів, розділяються на прості і складні. Зміна па площі покладу одного параметру (товщини, відкритої пористості і ін.) зображаються простою картою. Складна карта є результатом арифметичних і логічних операцій над простими полями. Виділяють два типа складних карт. Карти першого типу – результат композиції простих числових полів (карта питомих запасів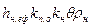 
), другого типу – результат композиції числових і логічних полів (карта питомих запасів колекторів різної продуктивності і ін.).
На основі вихідних даних по кожному під рахунковому об’єкту в кожній свердловині нафтового покладу в першу чергу обраховуються середні значення коефіцієнту відкритої пористості, нафтонасиченості і параметрів нафти. Для геометризації покладів по даних пробуреної сітки свердловин з використанням непрямої інформації або без неї використовують наступні блоки (набори алгоритмів), які відновлюють поля геологічних параметрів в вузлах щільної прямокутної сітки:
1) блок побудови простої арифметичної (числової) карти;
2) блок побудови логічної карти;
3) блок побудови складної карти;
4) блок інтегрування поля в заданій області довільної конфігурації.
При відновленні арифметичних полів застосовуються різні алгоритми інтерполяції в вузлах прямокутної сітки:
1) локальні лінійні поліноми (за Ю.В. Шуруборою, Г.Л. Русоковим і ін.);
2) локальні квадратичні поліноми (за Г.М. Дейнегою);
3) бікубічні сплайни (за А.М. Волковим, А.Н. Сидоровим, В.І. П’ятковим і ін.);
4) гармонічні функції (за В.І. Ароновим і ін.).
Яка з цих моделей найбільш задовольняє ту або іншу конкретну ситуацію, вирішує користувач, виходячи з апріорної інформації.
Без врахування непрямої інформації відновлюються числові поля відміток ВМГ по даних сейсмічних досліджень, коефіцієнтів відкритої пористості, пещаностості, нафто – (газо) насиченості і ін., а також логічні поля літології і ін.
Алгоритм відновлення логічних полів реалізується наступнім чином. Кожному вузлу щільної прямокутної сітки надається найменування ознаки, що спостерігається в найближчий свердловині (наприклад, колектор або не колектор) в результаті границі, які розділяють поля колекторів і не колекторів, проводиться по середині відстані між сусідніми свердловинами з різними значеннями ознаки.
З урахуванням непрямої і апріорної інформації можуть бути відновленні поля відміток покрівлі і підошви під рахункового об’єкту, відміток ВНК, ГВК, ГНК, нафтогазонасиченості при наявності перехідної зони, густини нафти, перерахункового коефіцієнта і ін. Для відновлення полів може бути використано люба з вище згаданих інтерполяційних моделей.
При побудові поля покрівлі пласта при незначній кількості свердловин в якості непрямої інформації використовується карта ВМГ по даних сейсмічних досліджень. Перехід з поля ВМГ, відновленого по даним сейсмопрофілів, на поле структури покрівлі пласта здійснюють за допомогою методу сходжень. Для цього попередньо складається карта, яка відображає різницю у відмітках ВМГ по даних буріння і сейсмічних матеріалів. Відніманням цієї карти з відновленого по даним сейсмопрофілів поля ВМГ отримують поле структури покрівлі пласта. Поле структури підошви пласта відновлюється по сумі (по модулю) полів структури покрівлі і загальної товщини пласта.
Для відновлення полів відміток ВНК (і інших контактів) використовується пряма і не пряма інформація. Прямою інформацією служать відмітки ВНК зафіксовані різними методами безпосередньо в проникному інтервалі пласта, до не прямої інформації відносяться відмітки підошви нижнього нафтонасиченого і покрівлі верхнього водонасичеого пропластків в свердловинах, де ВНК не встановлено. Вирішується ця задача методом послідовного наближення.
До складних полів відносяться поля загальної товщини покладу, натфто – (газо) насиченої товщини, питомих запасів. Ці поля відновлюються за допомогою математичних дій над складаючими їх простими полями. Так, поле загальної товщини покладу розраховуються як різниця між нижньою і верхньою границями покладу. В нафтовій зоні це поле отримується по різниці між відмітками підошви і покрівлі, а в водонафтовій зоні – між відмітками ВНК і відмітками покрівлі пласта. Поле нафтонасиченої товщини визначається в результаті добутку полів загальної товщини і коефіцієнтів нафтонасиченої товщини.
Найбільш складна задача при автоматизованому підрахунку запасів – відновлення поля нафтонасиченості при наявності в покладі перехідної зони.
|
Вихідними даними є середньо зважені по товщині пропластків значення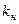 
, розраховані по кожній свердловині, в тому числі і в перехідній зоні. При відновлені поля 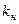значення, знайдені в вузлах прямокутної сітки за допомогою інтерполяції, повинні співпадати з встановленими в свердловинах, повільно змінюватися в оточеннях і поступово знижуватися до критичного значення 
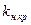на зовнішньому контурі покладу (рис 26.1).
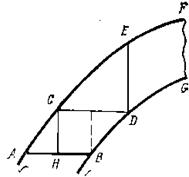
АВ – водонафтовий контакт; СD – поверхня стабілізації; CH, ЕD, FG – умовні лінії.
Рисунок 26.1 - Схематичний простір покладу, що пояснює геометризацію нафтогазонасиченості (за В.А.Бадяновим)
В межах фігури АСН величина нафтонасиченості визначається зміною товщини перехідної зони, в межах фігури HCEDB середньозважені значення параметру залежать від зміни товщини перехідної hн.п і стабілізованої hн.ст зон.
Таким чином, в межах покладу виділяються три області, в яких підходи до відновлення поля kн різні.
В нафтовій частині покладу, правіші лінії ED, відновлення поля kн здійснюється з врахуванням апріорної інформації. В якості останньої використовується модель зміни kн в перехідній зоні з збільшенням відстані l від дзеркала води, запропонованої В.М. Дахновим:
,
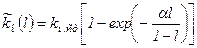де l – висота від дзеркала води, нормована на товщину перехідної зони, м;
kн.ст – середнє значення по свердловинах kн в стабілізованій зоні;
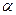- оцінюваний параметр функції.
Величина коефіцієнту нафтонасиченості в любій точці перехідної зони kн.п визначається наступним виразом: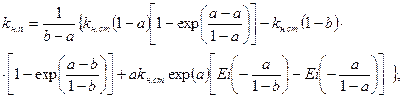 
В першу чергу інтерполяцією відновлюються поле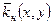 
по даних всієї чисельності свердловин. Для нафтової зони покладу, правіші лінії ED, це остаточні результати.
В межах ACDB відновлюється поле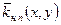 
, а потім знаходиться поле коефіцієнта нафтонасиченості 
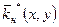в зоні AСЕDB.
,
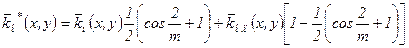де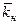 
- значення 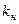в свердловинах, що пересікають перехідну зону;
m – апріорний параметр, що задається ваговою функцією.
Це остаточний результат для зони, обмеженою фігурою НСЕДБ.
Останнім відновлюється поле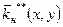 
для зони ACH. Остаточний результат для неї знаходиться по формулі
,
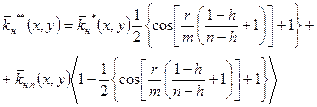де h – загальна товщина нафтового покладу, нормована на відстань від
ВНК до точки стабілізації;
r – відстань від вузлової точки до найближчої свердловини, м;
.
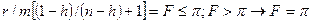І на завершення в вузлах, що співпадають з точками спостережень, отримають рівність відновленої і заданої величини 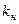, а також дотримання перерахованих вище умов.
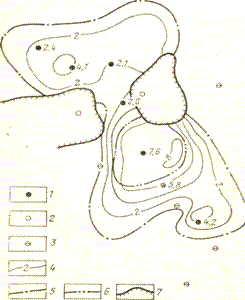
У випадку літолого – фаціального заміщення колекторів непроникними відмінностями пласта поля коефіцієнта нафтонасиченої товщини відновлюється тільки в зоні розповсюдження колекторів. Поле нафтонасиченої товщини знаходиться як добуток трьох полів: загальної товщини, коефіцієнтом нафтонасиченої товщини і літології (рис 26.2).
|
Свердловини:1-нафтові, 2- з відсутністю колекторів, 3-водяні;4- ізолінії товщин,м; контури нафтоносності: 5-зовнішні, 6-внутрішні; 7-зони відсутності колекторів
Рисунок 26.2 - Карта ефективних нафтонасичених товщин, виконана на ПЕОМ (за В.А. Бодяновим, Т.А. Бохан, Г.Я. Демуре та ін)
Складне поле питомих запасів нафти розраховується шляхом добутку полів нафтонасиченої товщини, коефіцієнтів відкритої пористості, нафтонасиченості і параметрів нафти. Поле питомих запасів розчиненого в нафті і газі відновлюється шляхом добутків полів питомих запасів нафти і початкового газовмісту, поле питомих об’ємів вільного газу – шляхом добутку середніх значень параметрів газу на полі газонасиченої товщини і коефіцієнтів відкритої пористості і газонасиченості.
Запаси нафти, вільного і розчиненого газу визначаються в результаті інтегрування даних про питомі запаси в вузлах прямокутної сітки х врахуванням масштабу малюнку.
З метою більш повного обліку кількості запасів при детальному проектуванні розробки методика підрахунку запасів на ПЕОМ передбачає також диференціацію запасів по площі і розрізу. При цьому розрізняють природну і штучну диференціацію. Різновидом площинної природної диференціації є оцінка параметрів і запасів різних зон покладів: нафтової, водонафтової і ін. Локалізація зон здійснюється за допомогою логічних операцій над полями структури покрівлі і підошви пласта, відміток ВНК, ГВК, ГНК. В іншому диференційована оцінка середньо зважених параметрів і запасів подібна вище описаної.
Природна диференціація по розрізу по суті є основою для виділення під рахункових об’єктів. Площинна природна диференціація параметрів і запасів по літологічним типам порід (пісковик, алевроліт, і ін.) здійснюється „накладанням” літологічного поля на диференційовані поля параметрів і запасів. В результаті в кожному вузлі прямокутної сітки приписується певну прикмету породи. Сумуючи значення запасів, що відповідають вузлам з однаковими прикметами породи, отримують запаси колекторів даного типу.
Штучною площиною диференціацією передбачається розподіл покладу на зони різних категорій запасів, елементи розробки, на геоморфологічні зони і ін. Поклад розбивається на зони замкнутими багатокутниками, границі яких задаються точками у вершинах багатокутників. Потім вирішується питання приналежності кожного вузла сітки до тої або іншої зони, для якої підраховується запас.
ЛЕКЦІЯ №27
