Принципиальная электрическая схема

Рис.9.9

 

Схема расположения приборов на панельном щитке

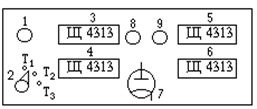Рис. 9.10

1 – тумб­лер вклю­че­ния в сеть ус­та­нов­ки; 2 – пе­ре­клю­ча­тель ре­жи­ма тем­пе­ра­тур ка­то­да; 3,4,5,6 – циф­ро­вые при­бо­ры Щ4313 для из­ме­ре­ния на­пря­же­ния и силы то­ка на ано­де и ка­то­де со­от­вет­ст­вен­но; 7 – ва­ку­ум­ный ди­од; 8,9 – по­тен­цио­мет­ры.

На при­бо­ре Щ4313 (3) - на­жа­ты кноп­ки "_~", "Y", "5"; ос­тальные от­жа­ты.

На при­бо­ре Щ4313 (4) – на­жа­ты кноп­ки "_~", "mA", "500"; ос­тальные от­жа­ты.

На при­бо­ре Щ4313 (5) – на­жа­ты кноп­ки "Y", "500", ос­таль­ные от­жа­ты.

На при­бо­ре Щ4313 (6) – на­жа­ты кноп­ки "mA", "5" или "0.5", ос­таль­ные отжа­ты.

Руч­ки по­тен­цио­мет­ров 8 (точ­но) и 9 (гру­бо) – в край­нем ле­вом по­ложе­нии (про­тив ча­со­вой стрел­ки до упо­ра).

Пе­ред на­ча­лом ра­бо­ты оз­на­ко­мить­ся с ус­та­нов­кой и про­ве­рить пра­виль­ность вклю­че­ния при­бо­ров. Под­го­то­вить таб­ли­цы для за­пи­си ре­зуль­та­тов экс­пе­ри­мен­та и рас­че­та по форме 9.4.

 

Порядок выполнения работы

1. Пе­ре­клю­ча­тель 2 ус­та­но­вить в по­ло­же­ние Т₁.

2. Вклю­чить ус­та­нов­ку тумб­ле­ром "сеть" и дать про­греть­ся при­бо­рам 5 минут.

3. По приборам 3 и 4 измерить и записать напряжение накала U _к и силу тока I _к накала катода.

4. Снять за­ви­си­мость анод­но­го то­ка I _a от анод­но­го на­пря­же­ния U _а. На­пря­же­ние U _a из­ме­нять че­рез 1 В в ин­тер­ва­ле от 2 до 10 В; че­рез 10 В в ин­тер­ва­ле от 10 до 50 В; че­рез 25 В в ин­тер­ва­ле от 50 до 200 В.

5. Ре­зуль­та­ты за­не­сти в таб­ли­цу 9.4.

Таблица 9.4

Т1	Т2	Т3
I к, мА = U к, В =	I к, мА = U к, В =	I к, мА = U к, В =
U a, В	I a, А	U a,В	I a, А	U a, В	I a, А

 

6. Ана­ло­гич­но (пункты 3 и 4) по­вто­рить из­ме­ре­ния для ос­таль­ных тем­пе­ра­тур­ных ре­жи­мов ка­то­да (пе­ре­клю­ча­тель 2 в по­ло­же­ни­ях Т₂ и Т₃).

7. По­стро­ить гра­фи­ки зависимости I _a= f (U _a) для зна­че­ний Т₁, Т₂ и Т₃ .

8. Оп­ре­де­лить по графикам зна­че­ния то­ков на­сы­ще­ния I _нас для всех трех ре­жи­мов ра­бо­ты, ре­зуль­та­ты за­не­сти в таб­ли­цу 9.5.

 

9. Оп­ре­де­лить зна­че­ние плот­но­сти то­ков на­сы­ще­ния: j _нас= I _нас/ S (S=4.83 мм²).

10. Вы­чис­лить со­про­тив­ле­ние катода R _к и тем­пе­ра­ту­ру Т для всех ре­жи­мов ра­бо­ты ка­то­да по фор­му­ле (9.6):

, (9.6)

где – сопротивление катода, нагретого до тем­пе­ра­ту­ры Т, R _o=1.5 Ом – со­про­тив­ле­ние ка­то­да при ком­нат­ной тем­пе­ра­ту­ре; Т ₀= 300 К.

Таблица 9.5.

№	I нас, А	j НАС, A/м2	I К, мA	U К, В	R К, Ом	Т, К	x =(1/ Т), К-1

 

11.Рас­счи­тать ве­ли­чи­ны x =(1/ Т) и для всех зна­че­ний температур.

12. По­стро­ить гра­фи­к зависимости y=f (x)(рис.9.11):

Рис.9.11

 

13. Определить тангенс угла наклона α полученной прямой к оси абсцисс и рассчитать работу выхода по формуле (9.5): 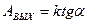. Все данные занести в таблицу 9.6.

14. Сде­лать вы­во­ды.

Таблица 9.6

	, К-1	, К	, Дж	, эВ

 

 

Контрольные вопросы

1. Что называется работой выхода электрона из металла? От чего она зависит?

2. Какова природа сил, препятствующих выходу электрона из металла?

3. Что такое термоэлектронная эмиссия?

4. Что такое вакуумный диод? Из чего он состоит?

5. Нарисуйте схему включения диода.

6. Нарисуйте и объясните вольтамперные характеристики диода. Почему характеристики нелинейны?

7. Что такое ток насыщения и как он зависит от температуры?

8. Сформулируйте закон «трёх вторых». Объясните его физическую природу и область применимости.

9. На­пи­ши­те фор­му­лу Ри­чард­со­на-Деш­ма­на, объ­яс­ни­те ее смысл и ха­рак­тер вы­ра­жае­мой ею за­ви­си­мо­сти, а также область её применимости.

10. Объ­яс­ни­те при­ме­няе­мый гра­фоана­ли­ти­че­ский ме­тод оп­ре­де­ле­ния работы выхода электрона из металла.

 

Используемая литература

[1] §18.5;

[3] §§ 5.10, 5.11, 5.12;

[5] §§ 104, 105.

Лабораторная работа 2-10

Изучение электрических колебаний в связанных контура (ФПЭ-13)

Цель работы – изучение обмена энергии в системе электрических контуров, слабо связанных между собой.

 

Теоретическое введение

Колебательные процессы (осцилляции) в электрических контурах имеют аналоги в механике. Поведение простейшего осциллятора – математического маятника, представляющего собой небольшое тело, подвешенное на длинном стержне, хорошо изучено: это гармонические колебания с частотой ω ₀.

Существенно более сложными являются колебания системы двух одинаковых маятников, связанных между собой слабой пружиной, как это показано на рис. 10.1. Маятники будут участвовать в коллективных колебаниях, вид которых зависит от мгновенной разности фаз смещений маятников (относительная фаза).

 

Если оба маятника вначале, при t= 0,одинаково сместить в одну и ту же сторону (рис.10.1,а), то они будут колебаться как единое целое с постоянной амплитудой и частотой, равными амплитуде и частоте колебаний одиночного маятника ω₀. Наличие пружины никак не повлияет на маятники, поскольку она останется недеформированной. Если при t= 0 имеются равные амплитуды и противоположные фазы (маятники сместили из положения равновесия в противоположные стороны на одинаковые углы, рис.10.1,б), то маятники будут колебаться с постоянной амплитудой и с частотой ω ₁, слегка повышенной по отношению к ω₀. Эти два вида движения называются нормальными модами колебаний системы связанных осцилляторов, причем вид колебаний с частотой ω ₀ называют четной модой нормальных колебаний и обозначают значком «+» (ω ⁺= ω₀), а вид колебаний с повышенной частотой ω ₁ называют нечетной модой нормальных колебаний и обозначают значком «–» (ω ^–= ω ₁). Нормальная мода колебаний – это коллективное колебание, при котором амплитуда колебаний каждой движущейся частицы системы остается неизменной.

В более сложных случаях, когда при t =0 имеется относительный сдвиг фаз, результирующее движение можно рассматривать как комбинацию (суперпозицию) двух нормальных мод колебаний. В результате такой суперпозиции (сложения) двух колебаний с разными частотами появляется амплитудно-модулированное сложное колебание. С такими колебаниями приходится встречаться в самых разнообразных явлениях. Примером могут служить не только маятники, но и два звучащих камертона с разными собственными частотами, причем наиболее интересным образом проявляются коллективные колебания, когда частоты колебаний камертонов мало отличаются друг от друга. В этом случае человеческое ухо воспринимает результирующее колебание как гармоническое колебание с переменной амплитудой (амплитудно-модулироаванный сигнал), то есть ухо слышит звук, интенсивность которого периодически меняется с частотой (частота биений) и периодом . Такой вид суперпозиции гармонических колебаний (при ω₀ ≈ ω ₁, но ω ₁> ω₀) иллюстрирует рис. 10.2. Само это явление называется биениями, а величины Т_δ и ω_δ – периодом и частотой биений соответственно.

В системе двух связанных слабой пружиной маятников биения могут установиться, если сместить один из них (например, маятник 1, рис. 10.1), удерживая первый на месте, а затем отпустить их одновременно. В этом случае маятник 1 начинает колебаться один (рис.10.2, t =0). С течением времени колебания маятника 2 будут нарастать, а колебания маятника 1 – затухать. Через некоторое время маятник 2 испытывает сильные колебания, а маятник 1 останавливается (рис.10.2, t = t ₁). Затем процесс происходит в обратном порядке: колебания маятника 1 нарастают, маятника 2 – затухают (рис.10.2, t = t ₂).

В случае четной моды нормальных колебаний маятники движутся вместе, пружина не растянута и частота такая же, как у одиночного маятника. В случае нечетной моды колебаний пружина деформируется, что увеличивает частоту этой моды колебаний. Если в какой-то момент времени смещён только один из маятников, то возникают две нормальные моды колебаний, находящиеся в определенной относительной фазе. Но поскольку частота нечетного колебания немного выше частоты четного колебания, относительная фаза медленно изменяется в процессе коллективного колебания. Амплитуда колебаний первого маятника оказывается равной нулю, а амплитуда второго достигает максимума, когда два нормальных вида колебаний окажутся в противофазе, затем начнется увеличение амплитуды первого маятника и т.д.

 

Поведение связанных осцилляторов можно легко объяснить с энергетической точки зрения. При t =0 вся энергия сосредоточена в маятнике 1. В результате связи через пружину энергия постепенно передается от маятника 1 к маятнику 2 до тех пор, пока вся энергия не окажется в маятнике 2. Затем, конечно, если система осцилляторов подпитывается извне энергией для компенсации затухания колебаний из-за трения, процесс обмена энергией повторяется от маятника 2 к маятнику 1 и т.д. Таким образом, “биения” – процесс обмена энергией между двумя гармоническими осцилляторами, собственные частоты которых различаются мало, а при t =0 наблюдается относительный сдвиг фаз .

Биения можно наблюдать и в электрической схеме – в двух одинаковых LC – контурах, связанных между собой слабой емкостной связью С_в – аналогом механической связи в виде пружины. Колебания в контурах возбуждаются с помощью преобразователя импульсов (ПИ) – см. рис. 10.3.

Экспериментальная часть

Приборы и оборудование: источник питания ИП; преобразователь импульсов ПИ; звуковой генератор PQ; осциллограф PO; магазин емкостей МЕ; модуль ФПЭ-13.

Функциональная схема представлена на рис. 10.5.

Методика измерений

Для теоретических расчетов рассмотрим упрощенный вариант этой схемы – рис. 10.4, где обозначены знаки зарядов с обкладок конденсаторов в контурах и положительное направление тока: С _в= С ₁₂; L ₁= L ₂= L, причем для наблюдения биений важно, чтобы I₁ и I₂ были сонаправлены. При одинаковом направлении токов знаки зарядов конденсаторов С ₁ и С ₂ окажутся такими, как указано на рис.10.4, а при равенстве этих зарядов конденсатор С ₁₂ окажется незаряженным. Таким образом, если в начальный момент Q ₁= Q ₂, то колебания в контурах будут происходить независимо, так как конденсатор С ₁₂ никакого влияния на колебания оказывать не будет. Такая ситуация аналогична колебаниям, возникающим в связанных математическиз маятниках, изображенных на рис.10.1,а.

Для двух LC – контуров, соединенных по схеме, показанной на рис. 10.4, запишем второе правило Кирхгофа для контуров ABEF и BCDE:

, (10.1)

. (10.2)

Подставляя , получаем:

; (10.3)

. (10.4)

Получилось довольно сложные уравнения для двух переменных. Можно упростить ситуацию, написать новые уравнения, полученные сложением и вычитанием уравнений (10.3) и (10.4).

Сложив эти уравнения, получаем:

. (10.5)

Разность (10.3) и (10.4) имеет вид:

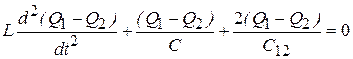. (10.6)

В (10.5) и (10.6) учтено, что С ₁= С ₂= С. Введём новые переменные:

и (10.7)

и обозначим:

и 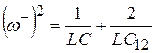, (10.8)

тогда в новых переменных (10.5) и (10.6) будут выглядеть так:

, (10.5а)

. (10.6а)

 

С помощью проведенных математических операций удалось свести уравнения (10.3) и (10.4) к более простым уравнениям относительно переменных и .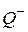

Если при t =0 переменная имеет значение , то решение уравнения (10.5а) имеет вид

(10.9)

частота

(10.10)

равна частоте собственных колебаний отдельного контура. Аналогично, решение уравнения (10.6а) приобретает вид:

(10.11)

где

; (10.12)

– значение при t =0 переменной .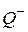

Два вида движения, описываемые уравнениями типа (10.5а) и (10.6а), называются нормальными модами колебаний системы связанных контуров, а переменные и 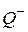– нормальными переменные. В данном случае эти уравнения описывают колебания тока в системе двух связанных электрических контуров. Нормальная мода колебаний – это коллективное колебание, при котором амплитуда колебаний каждого заряда и тока остается неизменной. Дифференциальные уравнения колебаний, записанные в нормальных переменных, имеют наиболее простой вид – это однородные дифференциальные уравнения второго порядка. Их решениями являются гармонические функции. Соответствующие частоты таких колебаний также называются нормальными.

Если вывести из положения равновесия один из контуров например, зарядить конденсатор С ₁), то результирующим колебанием будет наложение (суперпозиция) двух нормальных мод колебаний. При Q ₂₀=0 из (10.7), (10.9) и (10.10) получаем:

; (10.11)

. (10.12)

Используя известные тригонометрические тождества:

;

,

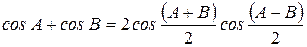можно записать уравнения (10.11) и (10.12) в виде:

; (10.13)

. (10.14)

Вид функций Q ₁(t) и Q ₂(t) (10.13) и (10.14) для случая слабой связи между контурами ( <<1) показан на рис. 10.2. В этом случае нормальные частоты и близки друг другу (10.10) и (10.12), и вторые сомножители в (10.13) и (10.14) изменяются достаточно медленно по сравнению с первыми, так как разность мала по сранению с суммой . Получается амплитудно-модулированный сигнал с амплитудой, изменяющейся с периодом (период биений) и основной частотой, совпадающей с резонансной частотой колебаний каждого контура – . При t =0 амплитуда Q ₂ равна нулю. Затем амплитуда Q ₂ увеличивается, а амплитуда Q ₁ уменьшается до тех пор, пока в момент времени, определяемый из соотношения 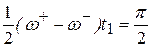амплитуда Q ₁ не станет минимальной, а амплитуда Q ₂ достигнет максимума.

Ситуацию, показанную на рис. 10.2, можно рассмотреть с энергетической точки зрения. При t =0 вся энергия сосредоточена в контуре 1. В результате связи через емкость С₁₂ энергия постепенно передается от контура 1 к контору 2 до тех пор, пока вся энергия не соберется в контуре 2. Время, необходимое для перехода энергии из контура 1 в контур 2 и обратно, можно получить из уравнения , а частота, с которой контуры обмениваются энергией

(10.15)

Для четной моды колебаний, обозначенной знаком «+», токи текут в одинаковом направлении и на емкости С ₁₂ нет заряда. При этом частота ω ⁺ остается такой же, как для несвязанных контуров, т.е. . В случае нечетной моды нормальных колебаний (знак «–»), емкость С ₁₂ заряжена, что увеличивает частоту колебаний, т.е. .

Следует отметить, что для того, чтобы применить к связанным контурам рассмотренную выше теорию, они должны иметь одинаковую резонансную частоту и, кроме того, предполагается, что С ₁₂ велика по сравнению с С, то есть <<1 («слабая связь»). Тогда выражение 10.15 можно преобразовать следующим образом

(10.16)

 

Полученное значение частоты обмена ω_обм (имеется в виду обмен энергией), или частоты “биений” ω _б= ω _обм можно изменять, настраивая систему контуров путем изменения номиналов элементов С, С ₁₂, L, R и т.д., добиваясь того, чтобы разностная частота была сведена к минимуму.

Исследование биений, то есть обмена энергий в связанных контурах, и является одной из практических задач данной лабораторной работы.