Цель работы: проверка закона Био-Савара-Лапласа на примере кругового тока и определение горизонтальной составляющей магнитного поля Земли.
Теоретическое введение
В 1820 году датский физик Х. Эрстед обнаружил, что проводник с током воздействует на магнитную стрелку. Вскоре Ампер установил взаимодействие параллельных токов и экспериментально доказал эквивалентность соленоида и постоянного магнита. Это позволило поставить задачу о сведении всех магнитных взаимодействий к взаимодействию элементов тока.
При истолковании магнитного взаимодействия токов будем исходить из теории близкодействия, согласно которой причина возникновения сил заключается в появлении вокруг проводников с током магнитного поля. Магнитное поле тока и оказывает силовое воздействие на магнитную стрелку или на другой проводник с током.
Для количественной характеристики магнитного поля вводится понятие индукции магнитного поля 
. Поле вектора можно представить графически с помощью линий индукции – линий, касательные к которым совпадают в каждой точке с вектором (рис.11.1). Число линий, проходящих через единичную площадку, перпендикулярно ей, численно равно величине вектора 
.
Ж. Био и Ф. Савар исследовали магнитное поле, создаваемое электрическим током, текущим по проводникам с различной конфигурацией и установили, что величина индукции магнитного поля пропорциональна силе тока.
Кроме того, она зависит от формы проводника, от расстояния и направления от проводника с током до исследуемой точки. По их просьбе П. Лаплас провел анализ полученных результатов и выяснил, что для магнитного поля, так же как и для электростатического, справедлив принцип суперпозиции:
. (11.1)
Здесь 
– величина индукции магнитного поля, созданного током I, текущим по элементарному участку проводника длиной dl. При этом элемент тока 
создает магнитное поле с индукцией:
, (11.2)
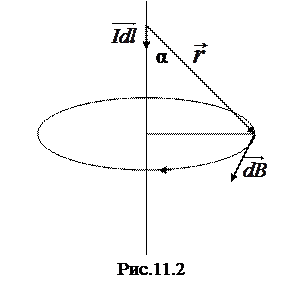где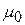 
– магнитная постоянная; r – расстояние от элемента тока до рассматриваемой точки (рис.11.2). Уравнение (11.2) получило название закона Био-Савара-Лапласа. Модуль вектора 
можно найти по формуле:
(11.3)
где a – угол между векторами 
и 
.
Таким образом, закон Био-Савара-Лапласа позволяет, если известна форма проводника, свести задачу определения индукции магнитного поля B, создаваемого проводником с током, к задаче суммирования элементарных индукций, согласно формулам (11.3) и (11.1).
Так, индукция B возле прямолинейного проводника в точке А
, (11.4)
где l – длина проводника; r – расстояние от проводника до точки А; I – сила тока, идущего по проводнику (рис.11.3).
Индукция B в центре кругового тока (рис.11.4)
, (11.5)
где R – радиус кругового тока; I – сила тока.
Индукция B на оси соленоида бесконечной длины
, (11.6)
где n – число витков на единицу длины соленоида.
Вычислим подробнее индукцию магнитного поля на оси кругового витка с током (рис. 11.5).
Элементарная индукция 
поля, созданного в точке А элементом тока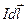 
, направлена по правилу правого винта перпендикулярно радиус-вектору 
, проведенному от элемента тока в точку А (рис.11.5), а её модуль можно найти из (11.3):
, (11.7)
где α=900 – угол между векторам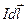и и . Разложим на две составляющих: 
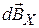– вдоль оси контура (ОХ) и 
– перпендикулярную оси ОХ, тогда
, 
. (11.8)
При сложении составляющих магнитного поля , перпендикулярных оси ОА, они компенсируют друг друга вследствие симметрии контура. Поэтому результирующая индукция магнитного поля в точке А направлена вдоль оси кругового тока и равна по модулю:
. (11.9)
Здесь учтено, что величины I, r, β постоянны, а интеграл по контуру 
равен длине окружности контура. Из рис.11.5 найдем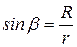 
, тогда:
, (11.10)
или:
. (11.11)
В частном случае, когда h =0, получаем формулу (11.5).
Экспериментальная часть
Приборы и оборудование: тангенс-гальванометр, амперметр, источник постоянного тока.
