Цель работы: измерение диэлектрической проницаемости твердых диэлектриков.
Теоретическое введение
Диэлектриками называют вещества, которые в обычных условиях практически не проводят электрический ток (удельное сопротивление диэлектриков r =106¸1015 Ом.м. При внесении диэлектриков во внешнее электрическое поле происходит их поляризация, вследствие чего в любом макроскопически малом его объеме D V возникает отличный от нуля суммарный дипольный электрический момент молекул. Количественной мерой поляризации диэлектрика является вектор поляризации (поляризованность):
, (1.1)
где 
– электрический дипольный момент i -ой молекулы, N – общее число молекул в объеме D V.
Опыт показывает, что в слабых полях, с которыми обычно имеют дело на практике, величина вектора поляризации 
пропорциональна напряженности 
электрического поля; вектор направлен так же, как и :
, (1.2)
где 
– диэлектрическая восприимчивость диэлектрика (безразмерная величина),
e0=8.85.10-12 Ф/м – электрическая постоянная.
В результате поляризации диэлектрика, помещенного в однородное электрическое поле, в тонких слоях, ограничивающих его поверхности, возникают не скомпенсированные связанные поверхностные поляризационные заряды σ′ (рис.1.1), а в неоднородном электрическом поле могут возникать еще и объемные поляризационные заряды. Согласно принципу суперпозиции, напряженность электрического поля в диэлектрике 
будет определяться векторной суммой напряженности внешнего электрического поля 
и напряженности поля 
, обусловленного не скомпенсированными поляризационными зарядами:
. (1.3)
Для изотропного диэлектрика, помещенного в однородное внешнее электрическое поле, эти векторы направлены в противоположные стороны, поэтому
, (1.4)
т.е. напряженность электрического поля в диэлектрике меньше напряженности этого поля в вакууме.
Напряженность поля связанных зарядов можно выразить через поверхностную плотность связанных зарядов (напряженность поля конденсатора):
. (1.5)
Поляризованность диэлектрика по определению (1.1) равна:
, (1.6)
где q ′= σ ′ S – величина связанного поляризационного заряда на всей поверхности диэлектрика, S – площадь обкладки конденсатора, l – расстояние между обкладками (толщина диэлектрика), q ′ l – электрический дипольный момент связанных зарядов, V = Sl – объем диэлектрика. (Предполагаем, что диэлектрик занимает весь объем конденсатора.)
Из (1.2), (1.4-1.6) получим:
,
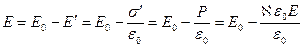откуда, решая уравнение 
, найдем:
.
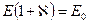Обозначим 
, тогда
. (1.7)
Величину e, численно равную отношению напряженности электрического поля в вакууме Е 0 к напряженности того же поля в диэлектрической среде Е, называют диэлектрической проницаемостью среды.
Согласно (1.4), e ³1 (e =1 для вакуума).
Экспериментальная часть
Приборы и оборудование: генератор переменного напряжения, электронный осциллограф, частотомер, микрометр и штангенциркуль, две металлические пластины, набор образцов диэлектриков, резистор с известным сопротивлением.
