1. Острый угол между прямой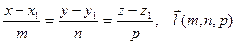 
и плоскостью 
, 
определяется по формуле:
.
2. Условие параллельности прямой и плоскости имеет вид:
Am+Bn+Cp=0.
3. Условие перпендикулярности прямой и плоскости имеет вид:
.
Пример1 (см. задание 1.3)
Найти угол между ребром А1А4 и гранью А1А2А3, если А1(2, 0,,3), А2(-1,0,8), А3(0, 2, 4) А4(0, 5, 6).
Решение.
1. Составим уравнение плоскости А1А2А3, как плоскости, проходящей через три точки (мы сделали это в предыдущем примере). Уравнение плоскости А1А2А3 имеет вид:
10x+7y+6z-38=0.
- нормаль к плоскости,
.
2. 
.
.
.
Пример 2(см. задание 1.8)
Составить уравнение высоты, опущенной из вершины А4 на грань А1А2А3.
1. Составим уравнение грани А1А2А3 (мы составляли его ранее – см. предыдущий пример).
10x+7y+6z-38=0.
- нормаль к плоскости.
2. Составим уравнение высоты, опущенной из А4.
Прямая 
плоскости А1А2А3, следовательно, нормаль к плоскости есть ее направляющий вектор 
.
Используем каноническое уравнение прямой в пространстве:
, А4(0, 5, 6).
-- уравнение высоты.
ВВЕДЕНИЕ В АНАЛИЗ
Пределы
1. Функция называется бесконечно малой при х→а, если 
.
2. Функция называется бесконечно большой при х→а, если она по модулю больше любого наперед заданного положительного числа.
Символическая запись:
.
3. Если f(x) – бесконечно большая функция при х→а, то 
-- бесконечно малая функция при х→а.
4. Если f(x)≠0 – бесконечно малая функция при х→а, то -- бесконечно большая функция при х→а.
Примеры
1) 
,
2) 
,
3) 
.
Неопределенность 
Чтобы раскрыть неопределенность такого вида, надо числитель и знаменатель почленно разделить на неизвестное слагаемое в наивысшей степени.
Пример (см.задание IV.а)
.
Для контроля следует помнить:
1) если степени многочленов в числителе и знаменателе равны, то предел равен отношению старших коэффициентов (коэффициент при высших степенях);
2) если степень числителя выше степени знаменателя, то предел равен бесконечности;
3) если степень числителя ниже степени знаменателя, то предел равен нулю.
Неопределенность 
1) 
,
где P(x), Q(x) – многочлены.
В этом случае надо числитель и знаменатель разделить на (х-а) один или несколько раз.
Пример (см. задание IV. b)
тогда 2x2-11x+5=2(x-x1)(x-x2)=2(x-5)(x-1/2).
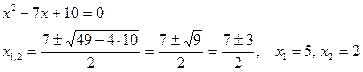
тогда x2-7x+10=(x-5)(x-2);
2) если и есть иррациональность, то числитель и знаменатель надо домножить на сопряженную величину.
Пример
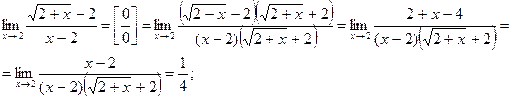
3) первый замечательный предел:
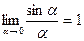
позволяет раскрывать неопределенность .
Следствия:
Примеры (см. задание IV.c)
1. 
.
2. 
.
Неопределенность 1∞
Неопределенность такого вида раскрывается с помощью второго замечательного предела:
.
Пример
