МАТЕМАТИКА
I часть
Методические указания и контрольные задания
для студентов МИППС первого курса технических специальностей
заочной формы обучения
Краснодар
Издательство КубГТУ
Составители:Горшкова С.Н., канд. физ.-мат. наук, доц.,
Данович Л.М., канд. техн. наук, доц.,
Арутюнян А.С., ст.преп.,
Наумова Н.А., ст.преп.,
Петрушина И.И., ст.преп.
УДК 517
Математика: Методические указания и контрольные задания для студентов МИППС первого курса технических специальностей заочной формы обучения/ Кубан.гос.ун-т; сост. С.Н.Горшкова, Л.М.Данович, А.С.Арутюнян, Н.А.Наумова, И.И.Петрушина.- Краснодар,2003г.
Приведены основные теоретические положения, даны необходимые формулы, разобраны типовые задачи, предложены контрольные задания.
Печатается по решению Редакционно-издательского совета Кубанского государственного технологического университета.
Рецензенты: Терещенко И.В., канд.физ.-мат. наук,
Алешин В.И., канд. техн. наук.
Программа курса высшей математики
Тема 1.Элементы векторной и линейной алгебры.
Определители второго и третьего порядков, их свойства, вычисление. Решение систем линейных уравнений методом Крамера. Матрицы, действия над ними, обратная матрица, решение систем линейных уравнений матричным способом. Векторы. Скалярное, векторное, смешанное произведения векторов, их свойства, приложения.
Тема 2.Элементы аналитической геометрии.
Прямая на плоскости. Различные формы уравнения прямой. Прямая в пространстве. Плоскость в пространстве. Их взаимное расположение.
Тема 3.Введение в анализ.
Понятие функции. Предел функции, основные теоремы о пределах. Бесконечно малые и бесконечно большие функции, связь между ними. Непрерывность функции. Свойства функций, непрерывных на отрезке.
Тема 4. Дифференциальное исчисление.
Производная функции, ее геометрический, механический и химический смысл. Основные правила и формулы дифференцирования. Производная сложной, обратной функции. Производные высших порядков. Теоремы о среднем. Правило Лопиталя. Условия монотонности функций. Необходимое и достаточное условия экстремума. Выпуклость и вогнутость, точки перегиба графика функции. Асимптоты. Общая схема исследования функции.
Тема 5. Функции нескольких переменных.
Понятие функции двух и более переменных. Область определения, пределы, непрерывность. Частные производные первого и второго порядков. Экстремумы функции двух переменных. Скалярное поле, градиент, производная по направлению, связь между ними.
Основная литература
1.Пискунов Н.С. Дифференциальное и интегральное исчисления. Том 1,2. М.: Наука, 1978 г
2. Шнейдер В.Е. и др./ Краткий курс высшей математики, / Шнейдер В.Е., Слуцкий И.А., Шумов А.С. - М.: Высш.шк., 1975 г.
Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1980 г.
Дополнительная литература
1. Игнатова А.В. и др. Курс высшей математики. М.: Высш.шк., 1964 г.
2. Каплан И.А. Практические занятия по высшей математике. Харьков, 1965 г.
Справочная литература (задачники)
1. Клетеник Д.В. Сборник задач по аналитической геометрии. М.:Наука,1975 г.
2. Берман Г.Н. Сборник задач по курсу математического анализа. М.: Наука, 1964 г.
Линейная алгебра
Определители. Системы
Выражение вида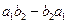 
называется определителем второго порядка и обозначается:
.
Рассмотрим систему:
,
где
-- главный определитель,
, 
-- вспомогательные определители. Они получаются заменой в главном определителе колонки коэффициентов при х (D1) и при y (D2) колонкой свободных членов.
Решение системы по правилу Крамера имеет вид:
.
Определителем третьего порядка называется число, обозначаемое символом
и вычисляемое по правилу Саррюса:
.
Произведение этих элементов Произведение этих элементов
берем со своими знаками берем с противоположными знаками
Для систем трех уравнений с тремя неизвестными
правило Крамера имеет вид:
,
где 
Пример (см.задание III)
Найти решение системы с помощью правила Крамера.
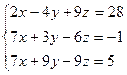
Решение.
.
Ответ: (2, 3, 4).
ВЕКТОРНАЯ АЛГЕБРА
Векторы
Вектором называется направленный отрезок прямой или упорядоченная пара точек (про которые известно, какая первая – начало, какая вторая – конец).
Обозначают: 
или 
.
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными: 
.
Если 
, то
1) 
- длина вектора;
2) 
;
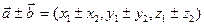3) 
, k - число;
4) 
.
Если заданы две точки A(x1, y1, z1), B(x2, y2, z2), то
1) 
2) если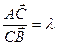 
, тогда координаты точки С, делящей отрезок в заданном отношении, находится по формулам:
В частности, если С – середина отрезка, то
.
Скалярное произведение двух векторов
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначается:
. (1)
Если заданы координаты векторов , то
, -
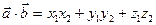координатная форма скалярного произведения.
Из (1) следует:
.
Пример (см. задание 1.1, 1.2)
Даны точки А1(1, -1, 2), А2(2, 1, 3), А3(-2, 4, 2).
Найти: 1) длины векторов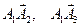 
,
2) угол между ребрами .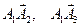
Решение.
Найдем координаты векторов:
=(2-1, 1-(-1), 3-2)=(1, 2, 1),
=(-2, 4-(-1), 2-2)=(-3, 5, 0).
Тогда длины векторов:
,
,
.
Тогда 
.
Замечание.
Если получите cos j=-a, где 0<a£1 (a-const), то j = p-arccos a.
Векторное произведение
Векторным произведением векторов и 
называется вектор 
, обладающий следующими свойствами:
1) 
;
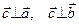2) 
;
3) вектор направлен так, как направлен винт при вращении его по кратчайшему расстоянию от первого перемножаемого вектора ко второму.
Из определения следует:
1) 
;
2) 
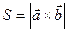- площадь параллелограмма, построенного на векторах и .
3) 
- площадь треугольника, построенного на векторах и .
Если заданы координаты векторов , то
или 
,
где 
- единичные векторы на осях ОХ, ОY, OZ.
Пример (см.задание 1.4)
Найти площадь грани А1А2А3, если А1(-1,2,0), А2(-2,0,4), А3 (-3,3,0).
Решение.
.
Тогда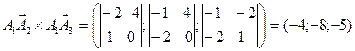 
.
.
Площадь грани равна: 
.
Ответ: .
Смешанное произведение
Если вектор умножить векторно на вектор , а потом получившийся вектор 
скалярно умножить на вектор , то полученное число называется смешанным произведением трех векторов.
Обозначается: 
.
Если известны координаты векторов 
, то
.
Можно доказать, что модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах 
, как на сторонах, т.е.
- объем параллелепипеда.
- объем пирамиды.
Пример (см.задание 1.5)
Найти объем пирамиды с вершинами А1(0,-1,2), А2(-1,0,6), А3(-2,1,0), А4(0,1,4).
Решение.
.
.
Тогда объем пирамиды:
.
Ответ: 
.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Прямая на плоскости
- каноническое уравнение прямой, проходящей через заданную точку A1(x1, y1), параллельно вектору 
.
- направляющий вектор.
- уравнение прямой, проходящей через 2 заданные точки A(x1, y1), A(x2, y2).
y-y1=k(x-x1) уравнение пучка прямых с центром A(x1, y1) и угловым коэффициентом k.
y=kx+b уравнение прямой с угловым коэффициентом.
A(x-x1)+B(y-y1)=0 уравнение прямой, проходящей через точку 
перпендикулярно вектору 
.
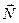- нормаль прямой.
После упрощения последнего уравнения получаем:
Ax+By+C=0 - общее уравнение прямой, где C=-(Ax1+By1).
Угловой коэффициент прямой находим по формуле 
.
Угол между двумя прямыми равен углу между их нормалями или направляющими векторами (см. скалярное произведение).
Если 
- угловые коэффициенты двух прямых, то
при 
- прямые параллельны,
при 
- прямые перпендикулярны.
Пример
Составить уравнение прямой, проходящей через точку М(3, 4):
а) параллельно прямой 2x-5y+1=0,
b) перпендикулярно прямой 2x-5y+1=0.
Решение.
а) 2x-5y+1=0; 
.
.
Если прямые параллельны, то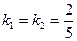 
.
Используем уравнение y-y1=k(x-x1), где 
, М(3, 4).
y-4= 
(x-3);
5(y-4)=2(y-3);
2x+5y+14=0.
b) Если прямые перпендикулярны, то 
.
;
;
.
Прямая в пространстве
каноническое уравнение прямой в пространстве, проходящей через точку A1(x1, y1, z1), параллельно вектору 
.
-- направляющий вектор.
Замечание. Если обращается в ноль одна из координат направляющего вектора, например m, то уравнение прямой принимает вид:
--
это прямая, лежащая в плоскости x=x1.
Если равны нулю две координаты направляющего вектора, например m=n=0, то уравнение прямой примет вид:
- эта прямая есть пересечение двух плоскостей x=x1 и y=y1, то есть параллельна оси OZ.
-- уравнение прямой, проходящей через две точки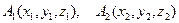 
.
Пример (см. задание 1.6)
Составим уравнение прямых А1, А2 и А1А3.
А1(2, 0, 3), А2(-1, 0, 8), А3(0, 2, 4).
Воспользуемся уравнением прямой, проходящей через две точки:
;
;
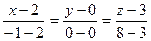-- уравнение прямой A1A2.
Эта прямая лежит в плоскости 
(т.е. в плоскости OXZ) и ее уравнение можно записать так:
.
Плоскость в пространстве
-уравнение плоскости, проходящей через точку 
, перпендикулярно вектору 
- нормали к плоскости.
-- уравнение плоскости, проходящей через три заданные точки 
.
Если две плоскости заданы общими уравнениями:
то по уравнениям двух плоскостей можно определить их нормали 
.
На основании теоремы об углах, образованных взаимно перпендикулярными сторонами, один из углов между плоскостями можно определить как угол между нормалями по формуле:
.
Пример (см.задание 1.7)
Составить уравнение плоскости А1А2А3, если А1(2, 0,,3), А2(-1, 0, 8), А3(0,2,4).
Воспользуемся уравнением плоскости, проходящей через три точки:
, 
, 
.
Раскроем определитель:
(x-2)∙0+y∙5∙(-2)+(z-3)∙(-3)∙2-(z-3)∙0-(x-2)∙2∙5-y∙(-3)∙1=0;
-10(x-2)-7y-6(z-3)=0;
-10x-7y-6z+38=0 –
уравнение плоскости А1А2А3.
