Алгоритм решения.
1. Прямую заключают во вспомогательную плоскость.
2. Строят линию пересечения заданной поверхности со вспомогательной плоскостью.
3. Линия пересечения с заданным отрезком прямой пересекаются, так как лежат в одной вспомогательной плоскости. Полученные точки (точка) пересечения и будут искомые.
Независимо от того, какая поверхность пересекается с отрезком прямой, алгоритм решения всегда одинаков.
Пример1. Построить проекции точек пересечения отрезка прямой а c октаэдром S. а Ç S = М, N (рис. 3.10).
Сначала надо построить проекции поверхности октаэдра S -проекции ребер, проходящих черезвершины ломаной направляющей A,B,C,D и точки E и F (рис. 3.11).
Видимость ребер можно определить визуально, без помощи конкурирующих точек. Вершина D, принадлежащая направляющей, расположена дальше других вершин этой же направляющей, значит, ребра FD и ED, проходящие через нее, будут относительно П2 невидимыми. Невидимыми относительно этой же плоскости проекций будут звенья направляющей AD и DC, а значит, и грани АED, AFD, DEC, DFC.
Относительно П1 видимыми будут те ребра и грани, которые расположены выше направляющей ABCD – DEA, CED, BEC, AEB.
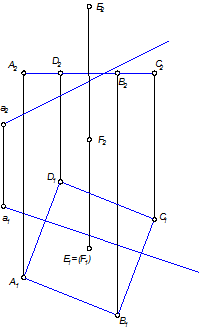
Рис. 3.10 Рис. 3.11
Решение.
1. Прямую а заключим во фронтально – проецирующую плоскость
L (а2 = L2). LÇSÞm – ломаная линия. Так как L // П2, следовательно, m2 Ì L2. (рис. 3.12).
2.Горизонтальную проекцию m построим по принадлежности ее октаэдру S, непроецирующей фигуре: точка 1 Ì AF, значит, точка 11 Ì А1 F1 ; точка
2 Ì АВ Þ 21 Ì А1 В1 и т.д.
3.Определим видимость линии m относительно П1. Видимыми будут те участки ломаной линии m, которые лежат на видимых гранях ABE, BEC, CED.
Отрезок прямой а и линия m принадлежат одной плоскости L, следовательно, они пересекутся в точках M и N: m Ç a = M, N.
4. Определим видимость пересекающихся фигур относительно друг друга.
Между точками М и N отрезок прямой на обеих проекциях невидимый, так как находится внутри поверхности S. Горизонтальная проекция отрезка до точки N1 видимая, потому что точка N лежит на видимой относительно П1 грани ВЕС. М1 – невидимая, значит, горизонтальная проекция а от М1 до А1D1 также невидимая, так как закрыта видимой гранью AED.
Рис. 3.12
Видимость отрезка прямой относительно П2 определяется аналогично.
Пример 2. Построить проекции точек пересечения отрезка прямой а с поверхностью тора S. а Ç S = М, N (рис. 3.13).
Сначала строим проекции поверхности тора S и проекции отрезка прямой а (рис. 3.14).
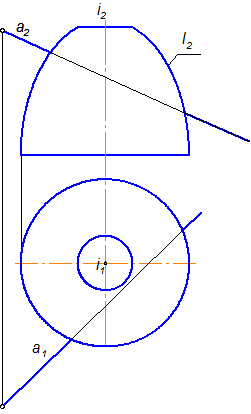
Рис. 3.13 Рис. 3.14
Решение .
1. Отрезок прямой а заключаем в горизонтально – проецирующую плоскость L, L1 = а1
Вспомогательная плоскость L пересекает поверхность тора S. Линия пересечения этих фигур – плоская кривая m:
S Ç L = m (рис. 3.15).
Так как L || П1 , следовательно, m1 Ì L1.
2. Фронтальную проекцию линии m строим по принадлежности ее непроецирующей поверхности S.
Построение любой кривой начинают с построения главных точек.
В данном примере главные точки: 1, 6 – оганичивающие кривую, 3 – высшая, 4 – определяющая границу видимости кривой m относительно П2. Остальные точки – промежуточные.
Фронтальные проекции большинства точек строим по принадлежности параллелям – окружностям, проекции которых на П2 вырождаются в отрезки прямых. Фронтальные проекции точек 1 и 6 строим по принадлежности линии обреза, точки 4 – по принадлежности очерковой образующей.
Высшая точка кривой при пересечении поверхности вращения с плоскостью лежит в осевом сечении поверхности, перпендикулярном секущей плоскости. Поэтому сначала выделяем точку 31 и при помощи окружности, касательной к L1 строим точку 32.
3. Видимость линии m относительно П2 определяем по принадлежности ее поверхности тора. Часть линии, проходящей через точки 1, 2, 3, и 4, будет видимой, так как лежит на видимой части поверхности.
Отрезок прямой а принадлежит L. Линия m также принадлежит L, следовательно, линия m пересекается с а в точках М и N, где М и N – искомые точки:
a Ì L; m Ì L Þ a Ç m = M, N
4. Определяем видимость пересекающихся фигур относительно П1 и П2 и относительно друг друга.
Между точками М и N отрезок прямой а на обеих проекциях будет невидимый. Относительно П1 эти точки видимые, значит, участки отрезка прямой, расположенные за ними будут видны. Относительно П2 точка М – видимая, значит, участок прямой до точки М2 также видимый, точка N – невидимая, участок прямой от N2 до очерковой образующей – невидимый, так как закрыт поверхностью тора.
Рис. 3.15
4.2.5. Примеры выполнения эпюра
