Любую поверхность вращения можно задать определителем, в состав которого входят ось вращения i и образующая l: S(i,l ). Алгоритмическая часть определителя заключается в названии. Т.е. название «поверхность вращения» означает, что каждая точка образующей l, вращаясь вокруг оси i, описывает окружность, плоскость которой перпендикулярна этой оси. Обычно ось поверхности вращения располагают перпендикулярно какой-либо плоскости проекций. Поэтому одна проекция окружности – параллели всегда представляет собой окружность истинного вида, а вторая проекция – есть отрезок, равный по длине диаметру окружности. Например, для точки A(A1 , A2 ) это окружность
с (с1 ,с2) (рис. 2.13).
Пример 1: Построить проекции поверхности вращения общего вида S(i, l), заданной проекциями геометрической части определителя (рис. 2.13). Построить горизонтальную проекцию линии а, принадлежащей поверхности.
Рис. 2.13 Рис. 2.14
Линия l – плоская кривая, расположенная в плоскости главного меридиана поверхности. Ось i ^ П1, поэтому горизонтальная проекция поверхности ограничена тремя окружностями.Это: n1 - горизонтальная проекция горла, m1 - горизонтальная проекция экватора и k1 - горизонтальная проекция окружности обреза. Фронтальные проекции этих окружностей вырождаются в отрезки. Это соответственно, n2, m2 и k2 (рис. 2.14).
Для построения линии l2¢ (левого полумеридиана)следует взять 8-10 произвольных точек. Обводим проекции поверхности с учетом видимости (рис. 2.15).
Для построения проекции кривой a(а1) на П1 необходимо взять несколько точек на a2 (порядка 6-8 точек) (рис. 2.16).
Построение линии a1 показано с учётом видимости кривой относительно плоскости П1, исходя из условия, что a2 задана как видимая.
Главными являются следующие точки: точки 1 и 6 – ограничивающие кривую, точки 3 и 5 – отделяющие видимые участки кривой от невидимых.
Рис. 2.15 Рис. 2.16
Пример 2. Построить проекции поверхности вращения общего вида Ф(i,l). Достроить недостающие проекции точек А, В, С (рис. 2.17).
Решение:
В этой задаче проекции образующей l(l1,l2) не лежат в плоскости фронтального меридиана, поэтому нам необходимо повернуть образующую так, чтобы она оказалась в одной плоскости с осью вращения.
Каждая точка образующей на П1, вращаясь вокруг оси i1, опишет траекторию окружности - параллель, на П2 ее проекция проецируется в прямую линию ^ i2.
1. Возьмем на образующей l(l1,l2) 6 точек (рис. 2.18).
Введем каждую точку в плоскость фронтального меридиана. Например, точка 1 опишет наибольшую, верхнюю параллель (экватор), точка 6 - наименьшую, нижнюю параллель (горло). Аналогичные построения проведем с остальными точками Þ правый полумеридиан.
2. Симметрично правому полумеридиану достраиваем левый (рис. 2.19). Обводим основной толстой линией проекции поверхности.
Рис. 2.17
3. Для построения недостающих проекций точек А, В, и С необходимо определить зоны видимости:
а) все точки, принадлежащие поверхности, относительно П1 будут видимы (изнутри).
б) видимость относительно П2 на рис. 2.20 показана заштрихованной зоной. Для построения горизонтальной проекции точки А(А1 ) необходимо:
- через точку А2 провести параллель радиусом R (от оси до очерка) (рис. 2.20);
- на П1 строим проекцию этой параллели радиусом R;
Рис. 2.18
- проводим линию связи от точки А 2 до пересечения с параллелью в заштрихованной зоне, т.к. точка А2 - видима;
- проекция точки А(А1 ) будет видимой.
Для построения точки В(В1) проводим аналогичные построения.
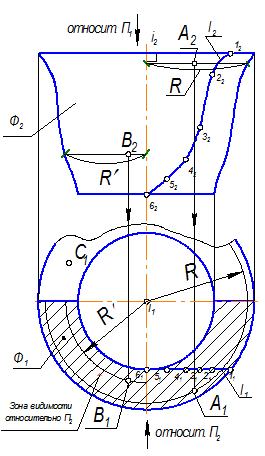
Рис. 2.19
Рис. 2.20
4. Горизонтальная проекция точки С1 расположена в незаштрихованной зоне, т.е. за плоскостью фронтального меридиана, следовательно, фронтальная проекция точки будет невидимой. На П1 через точку С1 проведем параллель радиусом R¢¢ до пересечения с горизонтальной проекцией
Рис. 2.21
левого полумеридиана в точке, которую обозначим звездочкой.
Построим фронтальную проекцию этой точки и проведем через нее фронтальную проекцию параллели, которой и будет принадлежать точка С2 (рис. 2.21).
Пример 3. Построить проекции конуса вращения Ф(i,l), у которого ось вращения занимает положение горизонтали. Линия а(а1) Ì F, а2 =? (рис. 2.22).
Для конусов вращения линия обреза задается окружностью.
Если ось вращения есть горизонталь или фронталь, то одна проекция окружности вырождается в отрезок прямой, перпендикулярный проекции оси и равный диаметру окружности. Другая проекция этой линии представляет собой эллипс. Большая ось эллипса занимает положение горизонтально проецирующей прямой. Малая ось эллипса занимает положение горизонтали.
Рис. 2.22
Разница между большой и малой осями эллипса не должна быть слишком большой или слишком малой. Поэтому угол наклона проекции к оси вращения рекомендуется задавать от 35 до 47°. Для более точного задания эллипса необходимо построить не менее 12 точек.
Очерковые образующие конуса следует проводить касательными к эллипсу, точки К2 и - точки касания. Чтобы построить проекцию линии а(а1) на П2 (а2) на а1 отмечают несколько точек (чем больше, тем точнее будет построена кривая), проводят через них образующие и находят их проекции на соответствующих образующих на П2 (рис. 2.23). Главными точками являются точки, принадлежащие очерковым образующим: 1, 6 и 8 и точка 5 – наивысшая точка. Точка 6 является границей видимости линии а на П2.
Рис. 2.23
Пример 4. Построить проекции поверхности кольца L(i,l). Обозначить проекции горла n(n1, n2 ) и экватора m(m1,m2), А(А2), А1 =? В(В1,) В2=? (рис. 2.24).
Каждая точка образующей на П1, вращаясь вокруг оси i1 опишет траекторию окружности - параллель, фронтальная проекция параллели проецируется в прямую линию ^ i.
1. Строим проекции правого полумеридиана (рис. 2.25).
2.Достраиваем симметрично проекции левого полумеридиана (рис. 2.26).
Рис. 2.24
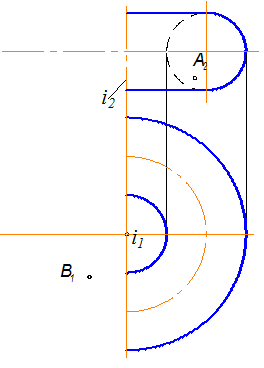
Рис. 2.25 Рис. 2.26
3. Строим недостающие проекции точек А и В. Определяем видимость этих точек относительно П1 и П2, обозначаем проекции горла и экватора (рис. 2.27).
Рис. 2.27
