К винтовым поверхностям относятся прямой и наклонный геликоиды. При построении этих поверхностей следует помнить, что они являются линейчатыми и на комплексном чертеже задаются дискретным каркасом.
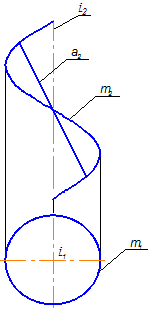
Пример 1. Построить проекции прямого геликоида. Геометрическая часть определителя прямого геликоида F (i, m), где i – ось, m - направляющая винтовая линия (рис. 2.28). Алгоритмическая часть определителя:
li Ç i, li Ç m, li ^ i, т.е. все образующие являются горизонтальными прямыми. Линия а(а2) Ì F, а1 =?
1. Дискретный каркас строим из 13 образующих, поэтому на горизонтальной проекции винтовой линии т берем 13 точек (рис. 2.29). Рис. 2.28
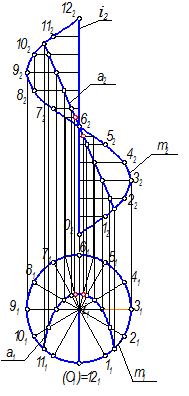Строим горизонтальную проекцию линии a, принадлежащей поверхности (рис. 2.30). На a2 отмечаем точки, принадлежащие образующим, и находим их горизонтальные проекции. Между образующими 6 и 5, 7 и 6 проведены дополнительные образующие, так как образующая, проведенная из точки 6, занимает проецирующее положение. Таким образом находим горизонтальную проекцию линии а, кривую а1.
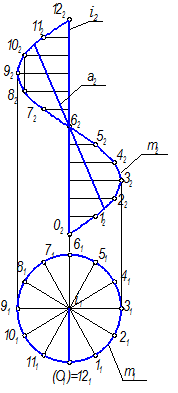
Рис. 2.29 Рис. 2.30
Методические рекомендации к решению задачи № 3
Чтобы решить позиционную задачу, нужно ответить на три вопроса:
1. Что? Определить, что будет являться общим элементом пересекающихся геометрических фигур (точки, ломаная линия, контур из плоских кривых, пространственная кривая и т. д.).
2. Сколько? Нужно знать характер пересечения геометрических фигур (чистое проницание, частный случай проницания – касание, вмятие).
3. Как? Выбрать соответствующий алгоритм решения, т.е. определить расположение пересекающихся геометрических фигур относительно плоскостей проекций (1 алгоритм, 2 алгоритм или 3 алгоритм).
Примеры решения 2 ГПЗ в случае, когда одна из пересекающихся фигур проецирующая, вторая – непроецирующая. 2 алгоритм
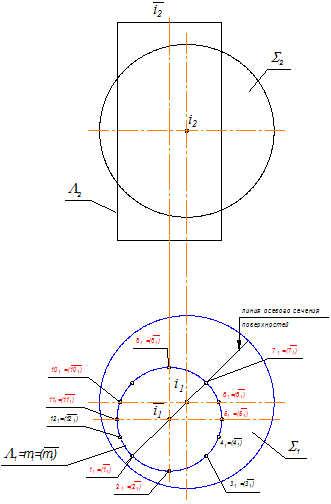
Пример 1. Построить проекции линии пересечения поверхностей сферы S и цилиндра вращения - L -. S Ç L = т (рис. 3.1).
Алгоритм решения:
S Ç L = т, 2 ГПЗ
L // П1, S – непроецирующая Þ 2 алгоритм
L // П1Þ m 1 =L1 ; m 2 Ì S2
Сначала строим две проекции сферы и недостающую проекцию цилиндра вращения (рис. 3.2).
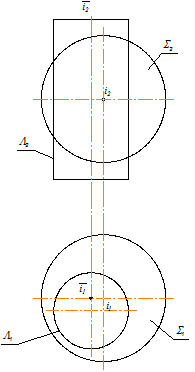
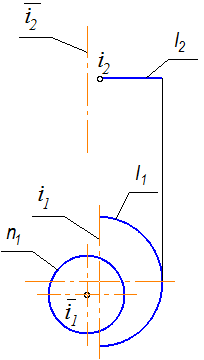
Рис. 3.1 Рис. 3.2
Вид пересечения – проницание. Значит, линий пересечения будет две:
S Ç L = m,. Обе поверхности являются поверхностями вращения второго порядка. Следовательно, при их пересечении получатся пространственные кривые второго порядка.
Решение.
Поверхность цилиндра L - проецирующая относительно П1 , следовательно, горизонтальные проекции двух пространственных кривых линий пересечения совпадают с горизонтальной проекцией (главной проекцией) цилиндра
m1, = L1
Фронтальные проекции обеих линий строим по принадлежности поверхности сферы.
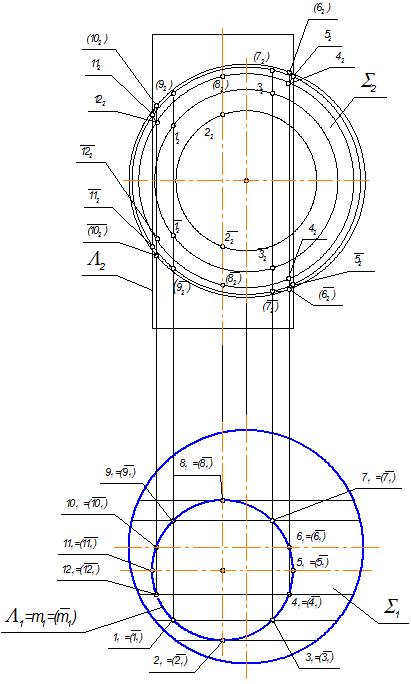
1. Начинать построение фронтальных проекций линий пересечения следует с главных точек. Такими являются точки 1 и 7 как высшие и низшие точки, лежащие в общем осевом сечении поверхностей вращения (горизонтальная проекция); точки 2, и 8, как самые ближние и дальние; точки 5, и 11, как точки, лежащие на границе видимой и невидимой частей линий пересечения (рис. 3.3). Выбираем несколько промежуточных точек.
Рис. 3.3
2. Для построения фронтальных проекций точек проводим окружности – параллели на поверхности сферы. Например, проводим окружность через точки 11 и 31 (рис. 3.4). Горизонтальная проекция такой окружности вырождается в отрезок прямой, перпендикулярный оси сферы. Радиусом, равным половине этого отрезка, строим ее фронтальную проекцию, которая на П2 изображается в истинном виде. Точки 12 и 32 принадлежат этой окружности.
Аналогично строим проекции всех остальных точек (и характерных и промежуточных) на П2.
Соединять построенные точки нужно в той же последовательности, что и на горизонтальной плоскости проекций, плавной кривой тонкой линией с последующей лекальной обводкой.
3. Решая вопрос видимости искомых линий относительно соответствующей плоскости проекций, надо помнить, что линии пересечения принадлежат обеим поверхностям одновременно. Поэтому видимыми будут те участки линий, 
которые лежат в зоне видимости обеих поверхностей относительно данной плоскости проекций (рис. 3.5).
Относительно П2 в зоне видимых точек будут лежать точки 11, 12, 1, 2, 3, 4, 5. Участки кривых, лежащих между точками 5, 6 и 10, 11, находятся в области видимых точек поверхности сферы, но невидимых точек поверхности цилиндра, поэтому будут невидимыми.
Рис. 3.4
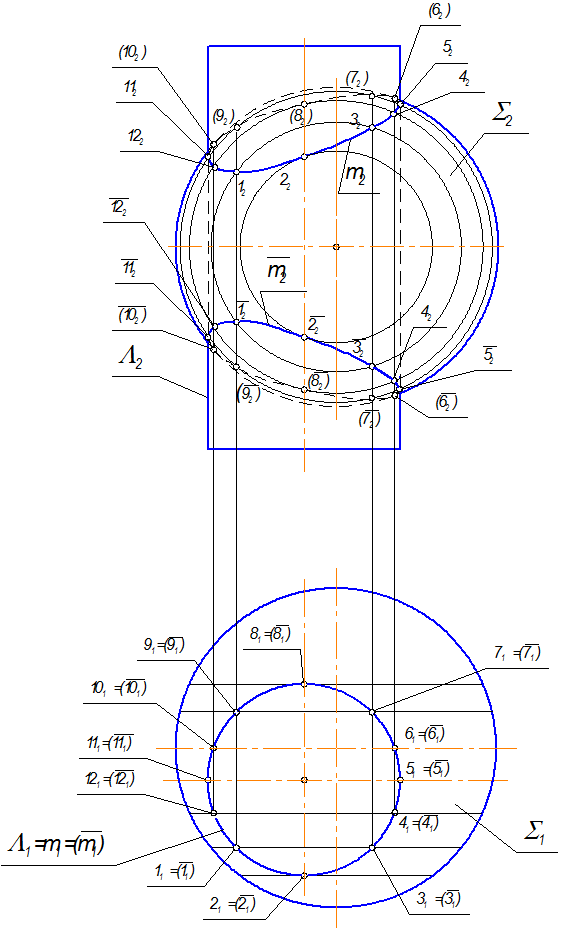
Рис. 3.5
Пример 2 Построить проекции линии пересечения поверхности эллипсоида вращения S с призматической поверхностью L (рис. 3.6).
Алгоритм решения:
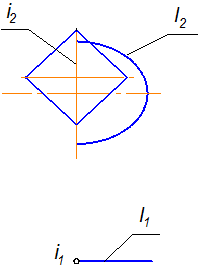S Ç L = т
S Ç L = т, 2 ГПЗ
L // П2, S – непроецирующая Þ 2 алгоритм
L // П2 Þ т 2 =L2 ; т 1 Ì S1
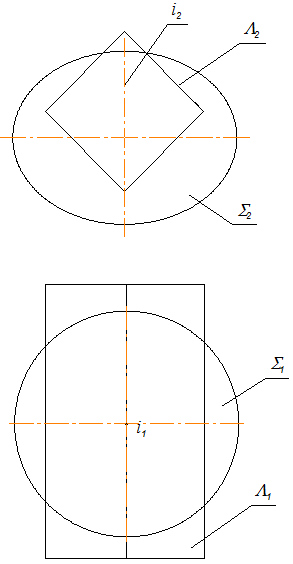
Рис. 3.6
Сначала строим две проекции эллипсоида и недостающую проекцию призмы (рис. 3.7).
После построения проекций поверхностей определяется вид пересечения. В данном примере вид пересечения – вмятие. Из этого следует, что линия пересечения – один замкнутый контур.
При пересечении эллипсоида одной гранью призмы линией пересечения будет плоская кривая - эллипс или дуга эллипса. А так как поверхность призмы состоит из четырех граней, то линия пересечения ее с поверхностью эллипсоида вращения представляет собой пространственный контур из плоских кривых – дуг эллипсов.
Рис. 3.7
Решение.
Горизонтальную проекцию линии m строим по принадлежности ее непроецирующей поверхности S, эллипсоиду вращения. Так как эллипсы на П1 симметричны относительно плоскости фронтального меридиана, то точки на П1 будем обозначать только в одной половине эллипсоида.
1. Сначала обозначаем главные точки линии пересечения (рис. 3.8).
Точки 1 и 1¢, 3 и 3¢, 6 – ограничивают линии пересечения (дуги эллипсов).
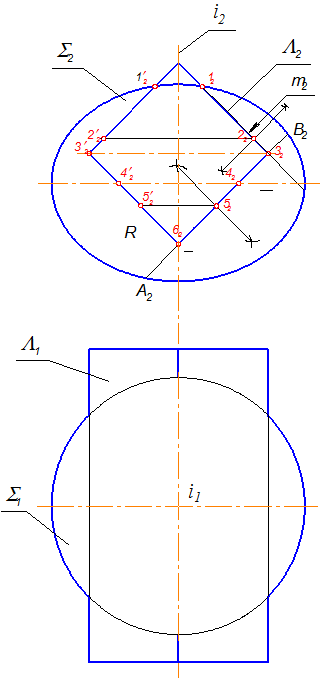Точки 4 и 4¢ принадлежат экватору эллипсоида.
Точки 2 и 2¢, 5 и 5 ¢ определяют большие оси эллипсов.
2. Рассмотрим построение одной из дуг эллипса, которая получается от пересечения грани k с поверхностью эллипсоида вращения (рис. 3.9). Фронтальная проекция ее совпадает с фронтальной проекцией грани. Малая ось эллипса определяется точками А и В, которые на П2 являются пересечением продолжения грани k с главным меридианом эллипсоида вращения.
Большая ось (на П2) вырождается в точку 5 и делит отрезок АВ пополам.
Точки пересечения ребер призмы с поверхностью эллипсоида – точки, ограничивающие дугу эллипса (3 и 6).
Рис. 3.8
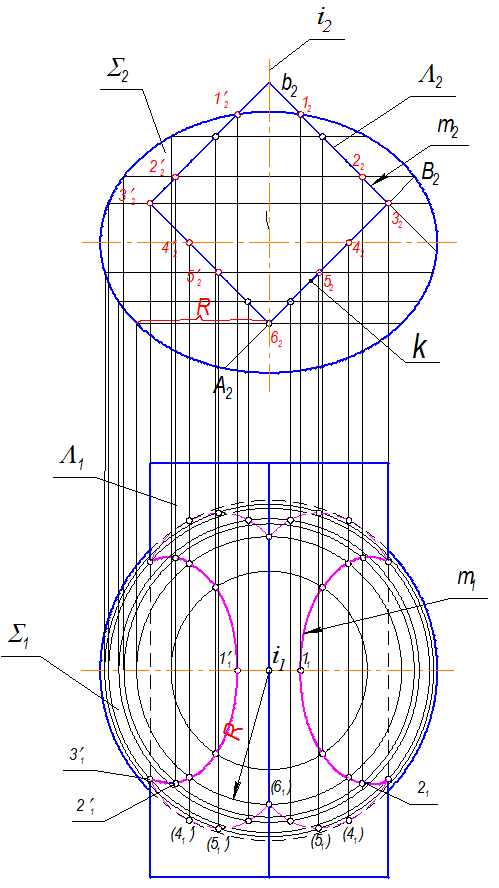
Рис. 3.9
Горизонтальные проекции этих точек, а также любых промежуточных строим по принадлежности параллелям эллипсоида. Например, точка 6 и ей симметричная лежат на параллели – окружности, фронтальная проекция которой вырождена в отрезок прямой, равный диаметру этой параллели и перпендикулярный оси вращения i2, а горизонтальная проекция – окружность в истинном виде.
Линии пересечения остальных граней с поверхностью строим аналогично.
Определение видимости линии пересечения двух поверхностей относительно П1 в данном примере сводится к определению видимости точек на поверхности призмы. Две верхние грани призмы видимые, поэтому и линии, принадлежащие им, видимые.
