Практична робота №4 Тема: Складання алгоритму знаходження максимального та мінімального значення функції на заданому інтервалі.

Мета Ознайомитисяз основними алгоритмами знаходження точок екстремуму на заданому відрізку.

Теоретичні відомості

Потрібно знайти точки мінімуму або максимуму функції у(х) на множині Q.

Загальна задача мінімізації формулюється таким чином:

Y→min

Потрібно знайти точку х, що задовольняє області допустимих значень Q і що доставляють мінімум функції у(х)

Цільова функція у(х) може мати декілька точок, в яких досягається мінімум.

Точка х* g Q називається точною глобального мінімуму функції у(х) на області Q, якщо у(х*) < у(х ) для всіх х є Q

Точка х* є Q називається точкою локального мінімуму функції на множині Q, якщо умова виконується тільки в малій околиці точки х*.

Глобальне рішення є і локальним, зворотне твердження невірне.

Завдання максимізації функції y(x) на області Q записуєтьсяу вигляді:

у (x)→ mах.

Ця задача еквівалентна наступній задачі мінімізації функції:

- у (x)→ min.

Задача одновимірної мінімізації формулюється таким чином:

Вважаємо, що точка мінімуму x* є [а, b].

Потрібно знайти точку мінімуму x* з точністю ξ на інтервалі [а,b].

Це задача пошуку екстремуму функції однієї змінної. Методи одновимірної мінімізації використовуються як самостійні методи оптимізації і як допоміжні в багатовимірних задачах оптимізації.

Як відомо, задача знаходження екстремуму функції у(x) зводиться до вирішення рівняння

у'(x) =0.

Вирішення рівняння не завжди вдається знайти в явному вигляді. Крім того, функція у(x) може виявитися такою, що не диференціюється.

У зв'язку з цим виникає необхідність в застосуванні чисельних методів.

Для вирішення задач одновимірної мінімізації використовуються методи, що не вимагають обчисляти похідних (пошукові методи).

Метод сканування (метод перебору).

Метод перебору є найпростішим методом мінімізації функцій однією змінною.

Хай точка мінімуму x* функції у(x) знаходиться на відрізку [а,b].

Для визначення x* з точністю ξ достатньо послідовно обчислити значення функції в точках

x_k=a+kξ, k=1,2,3… N=(b-a)/ξ

Потім вибирається крапка з найменшим значенням у(x_k).

Метод неефективний, якщо N - велике.

Більшість методів одновимірної мінімізації функції заснованs на припущенні про те, що функція у(х) задана на деякому відрізку [а,b] і має один мінімум.

Основними методами мінімізації унімодальних функцій є методи дихотомії і золотого перетину.

Метод дихотомії

На кожному кроці відрізок ділиться навпіл, і та його частина, в якій не може знаходитися точка мінімуму, відкидається.

При пошуку точки мінімуму функції у (х) методом дихотомії задаються: відрізок [а,b], на якому існує тільки одна точка мінімуму, та бажана точність ξ>0 рішень задачі.

Хай функція у(x) унімодальна (тобто має одну точку мінімуму), точка мінімуму функції знаходиться усередині відрізку [а,b]:

а < x* < b.

На першому кроці початковий відрізок ділиться навпіл:

Для того, щоб визначити, з якого боку від цієї точки знаходиться мінімум, потрібно обчислити значення функції в точках

Якщо точка мінімуму знаходиться зліва від потрібно відкинути праву частину відрізку, інакше відкидається ліва частина. Відрізок, що залишився, також ділиться навпіл, і проводяться аналогічні обчислення.

Процес пошуку мінімуму триває задане число разів або до тих пір, поки відрізок, що містить точку мінімуму, не стане менший або рівний ξ.

Після закінчення обчислень знайдена точка мінімуму буде відрізнятися від точного розв’язку не більше ніж на ξ.

Рис.1 Графічне зображення методу дихотомії.

Недоліком методу дихотомії є те, що на кожній ітерації методу значення функції у(х) потрібно обчислювати в двох точках х1,х2. Це недолік усувається в методі золотого перетину.

Метод золотого перетину

Метод золотого перетину заснований на золотому перетині відрізку. Золотим перетином відрізку називається ділення відрізку на дві нерівні частини так, щоб відношення всього відрізку до більшої частини дорівнювало відношенню більшої частини і меншої.

Золотий перетин відрізку [а,b] проводиться двома симетрично розташованими точками x ₁і x₂.

Алгоритм методу золотого перетину має наступний вигляд.

Рис.2 Графічне зображення методу золотого перетину.

Характеристика методу

На кожному кроці, окрім першого, потрібне обчислення тільки одного значення функції, оскільки друге значення збігається із значенням, що вийшло на попередньому кроці, тому метод золотого перетину ефективніший, ніж метод дихотомії.

Метод дозволяє вирішити задачу з необхідною точністю ξ при меншій кількості обчислень значень функції, чим при методі дихотомії.

Після n обчислень функції у(x) всередині відрізку [а,b] точка мінімуму знаходитиметься усередині інтервалу

bn - an =(b - a)/ , де τ= 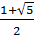≈ 1,618

Якщо точку мінімуму слід визначити з точністю ξ, то, отримавши інтервал [a_k, b_k ] довжиною не більш 2ξ, вважаємо, що мінімум – це середина відрізку.

Ефективність пошуку по методу золотого перетину рівна 1 /

Хід роботи

Побудуйте блок-схему для знаходження мінімального значення вказаної функції (згідно варіанту) на інтервалі від X_Н до X_К з точністю 0,0001. Метод пошуку обирається студентом довільно.

№ варіанта	Вид функції	Первинні данні
a	b	X_Н	X_К

	y =	-	0,75	1,35	6,5
	y =	19,6	7,8	14,6	34,8
	y =	1,38	-1,2
	y =	-	1,68	1,2	2,4
	y =	0,36	5,5
	y =	0,9	1,85		1,2
	y =	1,24	0,67	10,2	12,4
	y =	2,8	0,45
	y =	20,2	7,65	3,5
	y =	4,6	2,5	0,75	1,8
	y =	0,55	0,78	4,2	5,8
	y =	7,38	0,3
	y =	0,28	1,35	1,2	7,5
	y =	0,9	0,66	2,3	8,9
	y =	0,85	-	17,2	24,6
	y =	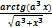1,16	-	0,25	1,28
	y =	0,4	10,8	0,84	1,25
	y =	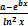1,28	0,03	12,6	34,9
	y =	0,25	0,68	11,6	15,8
	y =	1,6	1,24	0,2	1,4
	y =	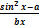1,8	0,34	6,44	9,1
	y =	0,44	2,28	6,5	7,3
	y =	3,2	0,45	0,6	1,5
	y =	17,6	10,4	1,9	3,8
	y =	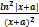8,24	-	14,9	24,8
	y =	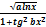7,32	0,05	13,3	14,5
	y =	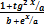4,1	0,05	1,25
	y =		-	0,6	0,02
	y =	1,35	0,98	7,5	26,6
	y =	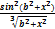-	2,5	1,28	5,34