Мета Навчитися створювати алгоритми пошуку коренів та давати їх графічне зображення за допомогою блок-схем.
Теоретичні відомості
Розглянемо рівняння вигляду:
f(x)=0
де f (x) – задана функція дійсного аргументу x, причому функція f (x) визначена і безперервна в деякому кінцевому або нескінченному інтервалі а< x<b.
Якщо рівняння достатньо складне, то його корінь рідко вдається знайти точно.
Тому розглянемо методи наближеного знаходження кореня рівняння.
Припускатимемо, що рівняння має лише ізольовані корені.
Наближене знаходження ізольованого дійсного кореня рівняння складається з двох етапів:
1) відділення кореня, тобто відшукання достатньо малих проміжків [а, b], в кожному з яких міститься один і лише один корінь рівняння;
2) уточнення наближеного кореня, тобто обчислення його із заданим ступенем точності.
Відокремлення кореня
Відділення кореня має на увазі встановлення можливо тісних проміжків [ а, b], в яких міститься один корінь рівняння.
Якщо безперервна функція f (x) набуває значень різних знаків на кінцях відрізку [ а, b], тобто f (a)*f (b) <0, то усередині цього відрізку міститься, щонайменше, один корінь рівняння, тобто знайдеться хоч би одне число x Є (а, b) таке, що f (x) =0.
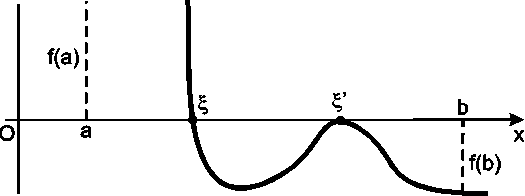
Рис. 1 Корені рівняння
Корінь x буде єдиним, якщо похідна f’(x) існує і зберігає постійний знак усередині інтервалу (а,b), тобто якщо f’(x) >0 (або f’(x)<0) при a<x<b.
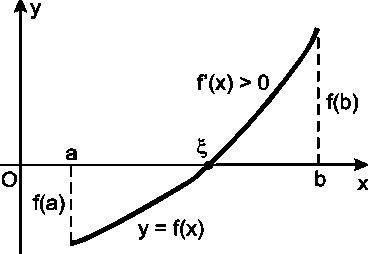
Рис. 2. Корінь рівняння
Процес відділення кореня починається зі встановлення знаків функції f(x) в граничних точках x =a і x =b області її існування. Потім необхідно визначити знаки функції f(x) у ряді проміжних точок x =a1, a2..., вибір яких враховує особливості функції f(x). Якщо опиниться, що f(ak)*f(ak+1) <0, де k=0 … N, то в інтервалі [ak, ak+1 ] є корінь рівняння.
Для відділення кореня практично часто буває досить провести процес половинного ділення, приблизно ділячи даний інтервал (а, b) на дві, чотири, вісім і так далі рівних частин (до деякого кроку) і визначаючи знаки функції f(x) в точках ділення.
Метод половинного поділу.
Хай дано рівняння
f(x)=0,
де функція f(x) безперервна на відрізку [а, b ] і f(a)* f(b) <0, і рівняння f(x) =0 має єдиний корінь на [а,b].
Потрібно знайти корінь рівняння із заданою точністю ξ > 0.
Алгоритм метод а повинного ділення знаходження кореня рівняння полягає в наступному.
Позначаємо a0=a, b0=b. Для знаходження кореня рівняння, котрий належить проміжку [a,b], ділимо цей проміжок навпіл точкою c0=(a 0+b 0)/2 і знаходимо значення f(x) в цій точці. Якщо f(с0) = 0, то х = c0 являється коренем рівняння і робота алгоритму закінчена. Якщо f(с 0) ≠0, то вибираємо ту з половин [a0,с0] або [с0,b0], на кінцях якого f(x) має протилежні знаки. Другий проміжок, котрий не містить кореня, відкидаємо.
В результаті вийде новий звужений відрізок [а 1, b 1 ], з яким необхідно провести ті ж дії, що і з відрізком [а, b ], і так далі.
Вказані дії повторюються до тих пір, доки або не буде знайдено точний корінь рівняння, або доки довжина проміжку [аk, bk ] не стане менше ξ. У цьому випадку коренем рівняння вважається середина знайденого проміжку.
Даний метод являється одним із найпростіших для реалізації, але при обчисленні з високою точністю проводиться досить великий обсяг обчислювальних робіт.
Хід роботи
Завдання.
Побудуйте блок-схему для обчислення значення аргументу функції У (згідно варіанту), для якого функція У перетинає вісь ОХ з точністю 0,0001.
| Варіант | Функція | Варіант | Функція | Варіант | Функція |
| У=х3-4х+5 | У=x3+2x4+12 | У=2x*sin(x-2) | |||
| У=3х5-6х-4 | У=sin(x)+cos(1-x) | У= х2+3.5sin(x) | |||
| У=3cos(3x-14)+3 | У=4sin(x-2)+6 | У=5sin(x-2)+3 | |||
| У=х7-3sin(x) | У=3х3-3х-14 | У=3-x3+4x2 | |||
| У=x+5x3-x2 | У=x4-3x2-14 | У=x2-sin(2x-4) | |||
| У=2sin(x-4)+1 | У=4cos(x-5)-1 | У=3x4-21x+4 | |||
| У=x+3-2x3 | У= 3х3-5х+11 | У=x3-x+3x2 | |||
| У=1.5х-5.6х4 | У=5x3-cos(x) | У=4cos(2x-5)+10 | |||
| У=3x2-5x+21 | У=4x+cos(x-3) | У=5х3-2sin(x) | |||
| У=cos(x+4)-sin(3x) | У=3x4-5x+4 | У=sin(3x)-cos(x) |
Контрольні запитання.
1. Які методи використовуються для наближених обчислень коренів нелінійних рівнянь? Дайте коротку характеристику цих методів.
2. Назвіть достатню умову існування кореня неперервної функції на проміжку.
3. Вкажіть часову складність алгоритму пошуку коренів методом двійкового поділу.






